一个铁匠收到了一件订单，要用一张边长为60厘米的正方形铁皮做一个没有盖子的铁盒，铁盒的盒底要是正方形的，而且容量必须是最大的。这个铁匠拿着尺子比画来比画去，想了好久也没有找到解决问题的方法，亲爱的读者，你可以运用你的数学知识得到问题的答案吗？

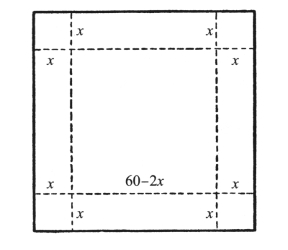
图73　问题图示

请看图73，假设各个边被折进去了x厘米，那么按照顾客的要求，正方形盒底的边长将等于（60-2x）厘米，铁盒的容积v=（60-2x）（60-2x）x。

我们现在解决的问题就是，当x是什么数时，（60-2x）（60-2x）x的乘积为最大值。

如果这三个乘数的和是一定的，那么这个乘积肯定是在三个乘数相等时是最大的。但这三个乘数的和：（60-2x）+（60-2x）+x=120-3x，并不是一定的，它随着x的变化而变化。但是我们可以使它们成为定值。只要把上式两边同时乘以4，就能得到：4v=（60-2x）（60-2x）4x。

这些乘数的和等于：

60-2x+60-2x+4x=120(www.daowen.com)

这个时候就是一个定值了，在这个情况下，三个乘数的乘积在三个乘数相等时达到最大值。

60-2x=4x，得出x=10

此时，4v达到了最大值，v也一定是达到了最大值。

这样，我们的铁匠知道应该如何处理这个订单了，他只要把铁皮的每一边折进去10厘米就能使铁盒的容积达到最大值。此时铁盒的容积为40×40×10=16000立方厘米。无论铁匠将铁皮多折还是少折1厘米，盒子的容积都会变小，不信你试试看：

9×42×42=15876立方厘米，

11×38×38=15884立方厘米。

无论是哪种情况，它们的容积都小于16000立方厘米。