在帕科姆的圈地问题中，我们在前文中仅讨论了矩形的可能性，那么他是否能够跑出其他的形状，比如三角形、四边形或五边形等等，而达到圈到更大面积土地的目的呢？

我们可以通过严谨的数学论证来解答这个问题，但这里我不并不打算这么做，我只准备将结果告诉你们。

首先，我们要证明，在所有周长相等四边形中，面积最大的是正方形。这一点我们已经在上文中证明过了。假定帕科姆圈到的土地是四边形的，同时他一天能够奔跑40俄里，那么他最多能圈到100平方俄里的土地，不能比这个更多了。因为边长为10俄里的正方形的面积是100平方俄里。

其次，我们要证明，在周长相等的条件下，正方形的面积比任何边长的三角形面积更大。周长同为40俄里的等边三角形，边长为俄里，那么根据公式

（式中S是面积，a是边长）计算，它的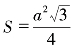面积就是平方俄里。这个面积甚至比帕科姆在小说中圈出来的面积还要小。

还有一个结论我就不在这里证明了，那就是在所有周长相等的三角形中，等边三角形的面积最大。假如面积最大的等边三角形的面积比正方形要小，那么，其他周长相等的三角形的面积必然比正方形要小。(www.daowen.com)

但是，如果我们跳出四边形的范围，看看五边形、六边形，那么情况就不同了，周长相同条件下，正方形不再具有优势。事实是，正五边形的面积要比正方形的面积大，而正六边形更大，以此类推。

我们来看看正六边形，周长还是40俄里不变，那么正六边形的边长就是俄里，它的面积根据公式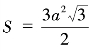计算，即是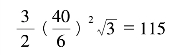平方俄里。

因此，如果帕科姆能够奔跑出一个正六边形，那么同样是奔跑40俄里的条件下，他可以得到更大的土地，超过了正方形面积的15平方俄里，当然这样的情况中，他需要随身携带一台测量仪。

如果我现在给你六根火柴，要求摆放出最大面积的图形。你会怎样做呢？

六根火柴可以摆出很多形状的图形，三角形、矩形、不等边的五边形还有正六边形，现在你已经知道以上的结论了，所以你可以毫不犹豫地摆出一个正六边形，此时的面积是最大的。