我们在前文中，已经看到了正方形的这种奇妙的特性，它的面积是周长相等的各种矩形中最大的，那么我们能不能给予数学上的证明呢？

我们用P表示一个矩形的周长，假设这个矩形是正方形，那么它的边长就是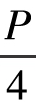，现在我们需要证明的就是：矩形的周长是一定的——把其中一个边长缩短长度b，把另一边增加长度b，这样得到的矩形的面积小于周长相等的正方形的面积。即是证明：

因为，那么这个不等式可以简化为：

0＞-b2或b2＞0

这个不等式是肯定成立的，因为任何非零数字的平方数都会大于0。因此原不等式也是成立的。

这样我们就能得出结论：在周长相等的条件下，各种矩形中正方形的面积最大。(www.daowen.com)

从这句结论中，我们还能得到一句话：在所有面积相同的矩形中，正方形的周长最短。

我们可以用反证法来证明，假设这句话是不正确的，那么就存在某个矩形A，它的面积和正方形B是一样的，但是周长比B的短。因此，如果用和矩形A相同的周长作一个正方形C，那么正方形C的面积应该比矩形A更大，因此也比正方形B的面积更大。

现在出现了什么情况呢？正方形C的周长比正方形B的周长要短，但是正方形C的面积却比正方形B的面积要大。这显然是不可能的，既然正方形C的周长比正方形B的周长要短，那么正方形C的边长也要比正方形B的边长短，面积自然也会要小一些。

因此，和正方形面积相同但是周长较短的矩形A是不可能存在的。换句话说，在所有面积相同的矩形中，正方形的周长是最短的。

可怜的帕科姆如果知道了正方形的这两个特性，就能够合理估量自己的能力以获得最大面积的土地而不会活活累死了。如果他能够一天之内轻松奔跑36俄里，那么他跑出边长为9俄里的正方形就能获得81平方俄里土地，这比他付出生命代价得到的78平方俄里的土地还要多3平方俄里。反过来看这个问题，如果他只计划得到36平方俄里的土地，那么他只需要跑出边长为6俄里的正方形就可以了，总周长仅为24俄里。