请看图56，把图中的五个图形画在一张纸上，要求每个图形既不能中断也不能重复，你能做到吗？

大部分拿到这个题目的人都是觉得图形d是最容易的，决定从这个图形开始，当他们拿起笔一试，就会发现自己失败了。但是他们会鼓起勇气作其他的尝试。出人意料之外的是，a和b并不难，很快就能描绘出来了，甚至是c图也比较容易画出来，只有d图和e图，没有人能够一笔把它们画出来。

问题来了，为什么有的图形能够一笔画出来，而有的图形不行呢？还是有些图形是根本不可能一笔画出来的，是否有什么方法能够提前判断一个图形是否能够一笔画出来？我们这样来解答这个问题：

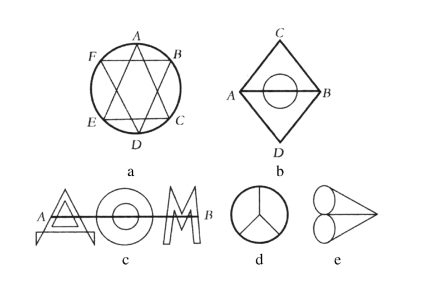
图54　请试着把图中的每个图形一笔画出

我们把每个图形中各个线条的交点称为“结点”。把有偶数条线会聚的结点称为偶结点；把有奇数条线会聚的结点称为奇结点。a图中都是偶结点，b图中有两个奇结点——A点和B点，C图中的奇结点是在中间横切的直线两端；d图和e图中各有四个奇结点。

我们先来看看所有结点都是偶结点的图形，比如a图。对于这种图形，我们可以从任意一点开始描画。当我们经过A点时，就能描出两条线：一条是离开这一点的，一条是靠近这一点的。从结点出来的线和进去的线条数目相同，所以我们每一次从一个结点画向另外一个结点的时候，还没有被画到的线条每一次就会减少两条，但是原则上画完所有的线条之后，可以回到出发点。

但是，如果画笔已经回到了出发点并且没有路再可以走了，但图形上还有没被描绘到的线条。假设这些由B点引出，而B点我们已经画过了。这就说明我们需要改变路线：在到达B点的时候，先画那些还没有画的线条，回到B点后再按原路程继续画。

比如我们想要一笔画出a图：先画出△ACE的三条边，然后回到A点后，画出圆周ABCDEFA，但是这样一来，△BDF就画不到了。因此我们要在离开B点、沿弧线BC描绘之前，先把△BDF画完。

到目前为止，我们就能发现，假如一个图形的所有结点都是偶结点，那么，无论从这个图形的哪一点出发，你一定可以一笔把它描绘下来，而且起点和终点是同一个点。(www.daowen.com)

现在让我们看看包含两个奇结点的图形的情况是怎么样的。比如b图，它有两个奇结点A和B，我们也能把这种图形一笔画出来。

请看图54中的b图，从A出发经过ACB达到B。把这些线条画过之后，每个奇结点都减少了一条线，那么奇结点也变成了偶结点。这个图形中就没有更多的奇结点了，图形就只有偶结点了。这样的图形和前面只有偶结点的情况是一样的，我们现在就可以用一笔画出整个图形了。

还有一点需要补充说明，当你从第一个奇结点开始画的时候，要选择合适的路径，不能出现和原有图形完全隔离的情形。比如图54的图b，如果从奇结点A出发沿AB直线直达另一奇结点B的时候，就错误了，这样圆周就和其他部分断绝了。一笔画就不可能实现了。

总而言之，假如一个图形中含有两个奇结点，那么正确的画法是从一个奇结点开始，在另一个奇结点终止，这就是说，画笔的起点和终点不会重合。我们从中也可知，如果一个图形有四个奇结点，比如图d和图e，这样的图形就不能一笔画出，而需要两笔。

从这一章中，我们应该看到，如果能够学会正确地思考问题，那么就可以预先知道许多事情，避免浪费不必要的精力和时间。比如在一笔画的问题上，你仔细观察图形之后马上就能断定一个图形是否可以一笔画出，而不会绞尽脑汁地想要去尝试画出并不能一笔画出的图形。不仅如此，你还能一眼看出应该从哪里开始画。

现在留给你最后一个问题，你能一笔画出以下两个图案吗？（图55）

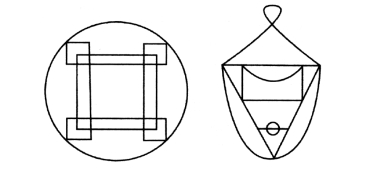
图55　你能把这两个图形一笔画出来吗