我们上一章的问题是如何只用直尺而不用圆规的情况下画圆，下面我们要看到的题目与上面的要求正好相反，只能用圆规而不能用直尺。

法国皇帝拿破仑曾经给法国的数学们出了一个题目：在已知圆心的条件下，不使用直尺，如何将一个圆周等分成四份？

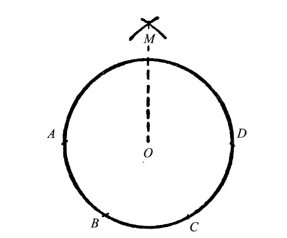
图50　只用圆规，如何把圆周分成四等分？

请看图50，假设要把圆周O分成四等分。从圆周上任意一点A出发，用半径的长度依次在圆周上作出B、C、D三点。显而易见，AC弧线是三分之一的圆周长，而AC直线则是内接等边三角形的一边，长度等于r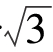，其中r是圆的半径。直线AD必然是圆周的直径。以AC为半径，从A点和D点分别作弧，则相交于M点。现在我们要证明的是，直线MO的长度恰好等于这个圆周的内接正方形的边长。

因为在△AMO中，直角边MO：

这也就是内接正方形的边长。(www.daowen.com)

现在，我们只要把MO的长度依次用圆规在圆周上划分，就能够得到圆周的内接正方形的四个顶点，这四个顶点将圆周分成了四等分。

还有一种与这个题目类似，但是要容易一些的题目。

问题是这样的，请看图51，如何不使用直尺，把A、B两点间的距离增加到五倍或者N倍呢？

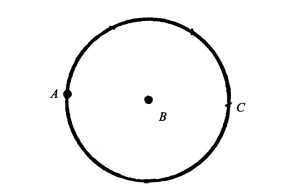
图51　只用圆规，如何把A、B两点间的距离增加到n倍（n是整数）

以B点为圆心，以AB为半径画一个圆。从A点出发，用AB的距离在圆周上依次量三次，我们就得到了C点，毫无疑问，这个C点就是在直径上和A点相对的一点。AC的长度是AB长度的两倍。

再以C点为圆心，以BC为半径画一个圆。这样又可以得到在直径上和B点相对的一点，也就是从A点出发，距离是AB三倍的一个点。以此推论，就能得到五倍或者N倍的长度。