题目:
图45中画着8个大小相同的圆形,其中7个画有粗黑线,都固定不动,第8个(细线的那个圆)紧贴另外7个无滑动地滚动,它绕这些固定不动的圆形一周,本身要转多少转呢?
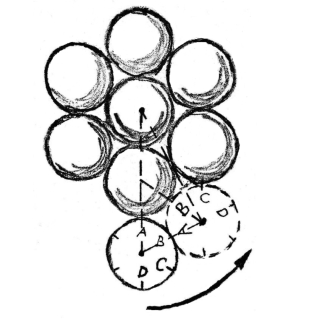
图45 1个圆绕另外7个圆转一周,本身要转几转?
我们当然可以马上用实践的方法得出这个题目的正确答案:把8个一模一样的硬币按照图中位置摆好,使7个“固定不动”的硬币在桌面上,让第8个绕着它们旋转。为了确定这个硬币的转数,你仔细留意硬币上数字的位置。每当这个数字转回到原来的位置,就表示它已经转了一转。你只要把这个实验切实做出来,就会知道这枚硬币一共转了4转。现在,我们开始用计算的方法来得出相同的答案。我们来看看,这个旋转着的圆形在每个固定不动的圆形上一共走了多长的弧线。为了达到这个目的,我们假设活动的圆形正由“顶点”向邻近两个固定圆形之间的“小凹地”间移动(如图45的虚线所示)。从图中可以看到,圆沿着滚动的弧线AB包含60°角。每一个固定的圆上有两个这样的弧线,两两相加就等于120°的弧线,或等于圆周的 。因此,滚动圆形在环绕了每个固定圆形的
。因此,滚动圆形在环绕了每个固定圆形的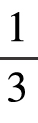 圆周时,也转了
圆周时,也转了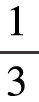 转。一共有6个固定圆形,可是活动圆形一共只绕了
转。一共有6个固定圆形,可是活动圆形一共只绕了 ×6=2转。
×6=2转。
这个答案和实验结果竟不一样,但是,我们要相信实验的结果。假如计算的结果和事实不一致,那就是计算中有错误。
请你把这个错误找出来。
回答:
当你把动圆沿着 圆周长的直线滚动时,这个动圆果然转了
圆周长的直线滚动时,这个动圆果然转了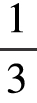 转。但是,假如这个动圆是沿着某种曲线的弧线滚动,那么刚才的说法就不正确了,与事实不相符。在这个题目中,那个动圆绕着相当于它的圆周长
转。但是,假如这个动圆是沿着某种曲线的弧线滚动,那么刚才的说法就不正确了,与事实不相符。在这个题目中,那个动圆绕着相当于它的圆周长 的弧线旋转时,一共走过的是
的弧线旋转时,一共走过的是 转,而不是
转,而不是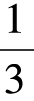 转,因此,当它绕过六个这种弧形的时候,就将转了6×
转,因此,当它绕过六个这种弧形的时候,就将转了6× =4转了!
=4转了!
这一点,你可以从以下的叙述得到证实。
图45的虚线表示动圆绕完定圆上的AB一段弧线(60°),就是等于全圆周长度六分之一的弧线时的位置。这个圆在它的新位置上,最高点已经不在A点,而在C点了,这就等于圆周上各点移动了120°,或移动了全转的 。定圆上120°的“路程”,将相当于动圆全转的
。定圆上120°的“路程”,将相当于动圆全转的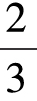 。
。
因此,如果这个圆形沿着曲线(或折线)绕转,那么它就要转出和沿同样长度的直线绕转时不同的转数。
我们还得再花一点时间在这个几何问题上,关于这一类问题的说明,常常令人难以置信。(www.daowen.com)
假定一个以r作半径的圆形,正沿一段直线向前滚动,它在和它的圆周同长(2πr)的直线AB上刚好转了1转。现在我们把这段直线AB在它的中心点C处曲折(图46),并把CD段折成和原来方向成α角。
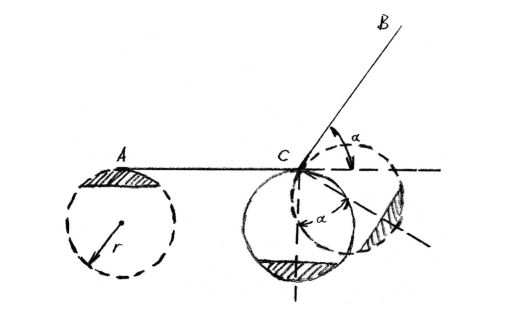
图46 圆形没有沿线段移动,在这里产生了多出来的旋转
于是,这个圆形在转了半转之后,就到达了顶点C,而且为了要转到CB线上去,它与它的圆心一起转了一个和α角相等的角度。
在这个旋转的过程中,圆形并不沿线段转动。正是在这里产生了比沿直线滚动多出来的转数。
这个多出来的旋转和全圆旋转相比,恰好跟α角和2π的比,就是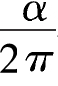 相同。圆形在CB上又转了半转,因此,这个圆形在整个折线ACB上,一共转了1+
相同。圆形在CB上又转了半转,因此,这个圆形在整个折线ACB上,一共转了1+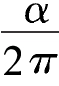 转。
转。
我们现在就能清楚知道,一个绕着正六边形外边旋转的圆形,绕完六边形各边后(图47),需要转多少转了。它的转数应该等于它在大边总长度的直线上所转的转数加上六个外角的和除以2π的商数。任何凸角多边形的外角总和总是等于2π,而 =1。
=1。
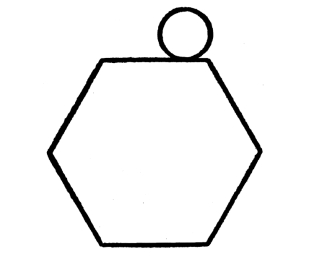
图47 圆形在多边形外滚动一周的转数比在相同周长的直线上滚动的转数多几周?
因此,圆形在六边形或任何多边形的外边滚动时,滚动一周的转数,必然要比它在这多边形各边总长相同的直线上滚动转数多一转。
一个凸角正多边形,当它的边数无穷增加时,就将和一个圆形接近,因此,我们刚才所讲的也适用于圆形。例如,假如把一个圆形放在另一个同样大小的圆形外面沿着一段120°的弧线上滚动,那么,这个滚动圆形要滚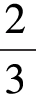 转而不是
转而不是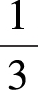 转。
转。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






