我们在实际运用中，使用的π的值通常为3.14或者。把一个圆的个直径量到一条直线上，就等于把这个圆周展开了。经验丰富的木工、铁匠们还有一套自己的方法来展开圆周，在这本书中，我就不一一介绍了。我有一种既简单又比较精确的方法介绍给亲爱的读者们。请看图123。

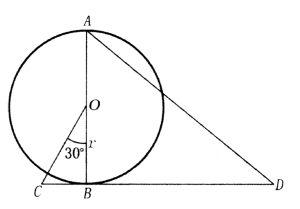
图44　将圆周展开的简易方法

如图44所示，如果我们要将一个半径为r的圆展开，我们首先要作出直径AB，然后经过B点作一条直线垂直于AB。然后再经过圆心O做一条与AB成30°角的直线OC。

从C点起，在CD上取一段等于三个半径的长度，把得到的D点和A点连接：AD的长度就等于半个圆周的长度。如果将AD的长度增加一倍，得到的就是圆周展开后的长度的近似值。用这种方法计算出来的误差不超过0.0002r。

下面我们就来证明一下。

根据勾股定理：

CB2+OB2=OC2。(www.daowen.com)

r表示半径OB，因为∠COB为直角三角形中的30°角，所以CB=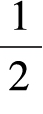OC。我们代入数值得出：

所以，

然后在△ABD中，

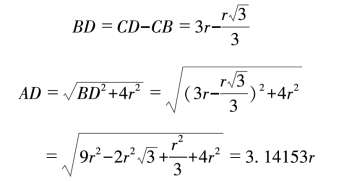
我们得出的这个结果与用π（采用的π=3.141593）计算出来的数值只差0.00006r，这个精确度是相当高的。假如我们用这个方法展开一个半径为1米的圆，那么半个圆周所产生的误差只有0.00006米，对于整个圆周来说也只相差0.00012米或0.12毫米，误差是非常小的。