马因·里德小说中的聪明少年所采用的方法是一种粗略的计算方法，只要有几何学基础的读者都能发现这一点。请看图42，其中，r表示小底面的半径，R表示大底面半径，h表示木桶的高度，也就是每个圆台高度的两倍。那么少年所得到的容积可以用下式表示：

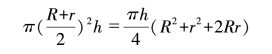
但是如果按照几何学的原理，我们所求的容积应该等于

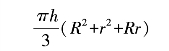
这两个式子计算出来的结果肯定是不一样的，而且容易发现，第二个式子计算出的结果要比第一个式子计算出的要大：

这个差值肯定是个正数，这说明少年计算出来的数值比实际情形要小些。究竟要少多少呢？一般来说，木桶最粗的部分比底面直径多出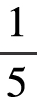左右，也就是R-r=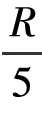，而小说中的木桶也是这样的形状，由此我们能够计算出，少年算出的容积与真正的容积之间的差距：

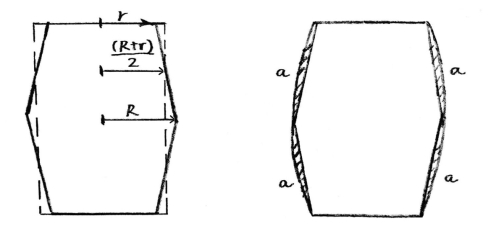
图42　验算木桶的体积

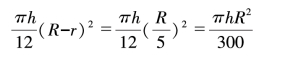
如果假设π=3，计算出来大约等于。这样看来，少年用自己的计算方法得到数值的误差有一个木桶最大截面的半径为底面半径、以木桶高的为高的一个圆柱体的容积那么多。

真实的情况比这个误差还要大一些，因为木桶的容积要比两个叠加在一起的圆台的容积大，这一点可以从图42中清楚地看出来。少年测量容积的时候，是将4个a点代表的阴影面积全部忽略了。(www.daowen.com)

上面这种简单计算木桶容积的方法并不是马因·里德书中的少年所独创的，很多介绍几何学的基本知识的课本中都有涉及，将其作为计算木桶容积近似值的简单方法介绍给读者。

我们知道，如果想要精确地计算木桶的容积可不是件容易的事情。17世纪时，著名的天文学家开普勒曾经专门研究过如何计算木桶的容积，并为此留下了数学专著。迄今为止，人们依旧没有发现简单而又准确的计算木桶容积的方法，简单的方法得到的都只是近似值，比如，在法国南部流行的计算木桶容积的方法就是如下的公式：

木桶容积=3.2hRr

这个公式在实际生活中是非常简便好用的。

不知道你是否考虑过这个问题，我们为什么要把木桶做成这种形状——中间逐渐拱起的圆柱体，而不做成规整的圆柱体或是正方体呢？这种形状的优势到底在哪里呢？

人们将木桶设计为中间凸起的圆柱体的形状是有原因的，这样的形状使人们很容易用锤子把桶箍牢牢地固定住，使木桶足够的牢固。

你知道发现行星运动规律的天文学家开普勒是怎样看待木桶容积这件地球上的小事情的吗？他甚至还特地为此写了一篇数学论文——《测量酒桶的新立体几何》，让我们看看他是怎样写的：

我们盛放红酒用的大木桶，根据实际使用以及制造材料上的需要，采用的形状既不是圆锥形也不是圆柱形，而是中间凸起的圆柱形。我们不能把酒放在金属容器中，因为这样容易腐蚀容器；玻璃器皿或陶瓷器皿不够大，不能存放大量的酒；而石头器皿又太重了，不容易搬起来，所以木头做成的桶是最适合储存酒的，人们从古代开始就用木桶来储存酒。大树砍掉后的树干，可以被挖空做成木桶，但是这样的木桶容量有限，而且树干粗大的树木也是有限的，所以我们看到的木桶都不是用一整棵树做的，而是用很多根木条捆在一起制作的。这样一来就有个问题需要解决，木条之间的缝隙怎么处理。如果不要液体流出来，那么只能用桶箍把木桶箍得紧紧的。

如果能够用木条拼接成球形那是最好的，但是对于木头这种材料来说不太切实际，因此只能考虑圆柱体，但是这个圆柱体不能是标准的圆柱形，因为这样一旦桶箍松了，那么整个木桶都将无法固定好。如果木桶是凸起的形状，那么当某处的桶箍松了，可以向木桶上较粗的地方移动。不仅如此，这样的桶形，还方便搬运，可以在地上滚动。而且模样也很圆润美观。

亲爱的读者可不要认为这是大科学家消遣时候写的小文章，开普勒为了验证这个问题，甚至把无穷小和微积分之类高等数学中的知识运用进来了，他将这个生活中的常见问题引申到了深奥的数学的高度。