地平线离我们有多远？如果观测者站在一片空旷地带的中心，以观测者所在的位置为中心画圆，这个圆圈的半径最大能够有多大？假设我们已知观测者的高度，那么如何计算出地平线离我们有多远呢？

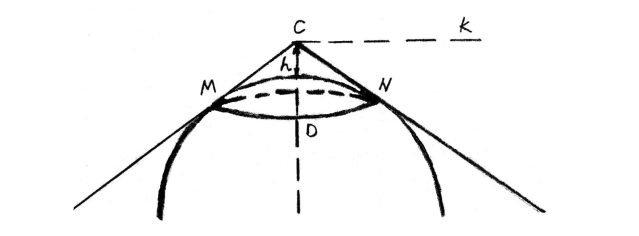
图39　关于地平线远近的题目的解法

请看图39，这个问题转换成数学图形，就是需要我们求得直线CN的长度，CN就是从观测者的眼睛向地表所作的切线。我们知道，切线的平方等于割线外段h和这条割线全长就是h+2R的乘积，其中R是地球的半径。与地球的直径比较起来，观测者的眼睛到地面的距离是非常微小的，小到几乎可以忽略不计。就算是一万多米高空中飞机上的乘客，他们的眼睛与地面的距离也只不过是地球直径（地球直径约为12756千米）的0.001，所以我们可以认为2R+h等于2R，这样公式就变为：CN2=h×2R。

这样一来，我们就能用这个简单的公式求得地平线和观测者之间的距离是，其中，A是地球半径，约为6400千米，h是观测者的眼睛和地面之间的距离。我们还可以对以上算式进一步简化，将6400的数值代入，我们可以得到：

地平线和观测者之间的距离，其中h的数量单位是千米。

这是经过简化之后几何计算方式，算出来的是一个大约的数据，如果我们想要得到一个非常精确的结果，我们还要考虑诸如“大气折射”之类的物理学因素的影响。一般来说，光线在大气中的折射作用对计算结果的影响大约增加在6%。6%只是一个平均数值，有很多客观条件会使这个数据发生变化，比如：

问题：

一个站在平地上的人最远可以看到多远？

回答：

假设这个成年人的眼睛距离地面1.6米，也就是0.0016千米，所以我们可以算出，人与地平线之间的距离是千米。

如前文所述，光线在大气层中会发生折射现象，距离会变大大约6%，考虑到这个误差，我们需要把4.52千米乘以1.06，得到：4.52×1.06=4.8千米。也就是说，这个成年人在平地上目力所能及得的距离不超过4.8千米，以他为中心的圆形面积为72平方千米。你是不是觉得比自己原本想象的要小得多？

问题：(www.daowen.com)

大海上有一艘小艇，坐在小艇上的人可以看到多远？

回答：

假设坐在这个小艇中的人的眼睛距离海面1米，也就是0.001千米，所以我们可以算出，人与地平线之间的距离是千米，如果将光线在大气层中会发生的折射考虑进来，那么这个结果大约是3.8千米。

如果观察者的眼睛距离海面更近，那么地平线的距离也就更近。如果观测者的眼睛距离海面只有0.5米，那么他与地平线的距离就是2.5千米。同样可证，如果观测者的眼睛与海面的距离增大，观测者看到的地平线也与之距离更远。比如，从4米高的桅杆顶眺望，地平线的距离就能达7千米。

问题：

如果一个飞行员想要看到以自己为中心的50千米半径的地面，他应该飞到一个什么高度？

回答：

我们用计算地平线距离的公式可以得出下列等式：

由此得出：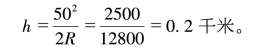

这说明，这位飞行员需要飞到0.2千米，也就是200米的高度。将6%的偏差考虑进去，从50千米中减掉6%，得47千米，因此：

这就是说，飞行员只要飞到170米的高度就能看到50千米半径的地面了。