作家果戈里曾经对第聂伯河有一段描写，“群星在黑色的夜幕中闪闪发光，它们的倒影全部落入了第聂伯河中，第聂伯河拥抱着它们，没有一颗星星能够逃脱，除非它们自己幻灭。”果戈里对于第聂伯河的描写既真实也富有文学性。当人们站在河岸边时，会感觉漫天的繁星都映照在河流中，但是河流中真的能看到所有的星星吗？

请看图28，MN是河水的水面，A是站在河岸边的观察者的眼睛位置，观察者从A点望向河面，可以看到哪些星星呢？

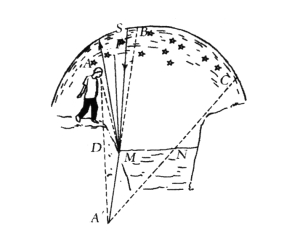
图28　在镜子里，你能看到哪一部分的星星

为了回答这个问题，我们从点A做一条垂直于MN的直线AD，并将AD延长到A'，使AD=DA'。如果观察者的眼睛位于点A，从A点仰望星空，他能看到的实际上是∠BA'C以内的星空，位于∠BA'C以外的星星，观察者实际上是看不到的。

我们应该如何证明这一点呢？如何证明观察者在河中其实看不到∠BA'C之外的星星呢？比如，如何证明我们无法看到星星S呢？(www.daowen.com)

我们根据光的反射定律，将S投射到离河岸比较近的M点的光线路径作为研究对象，S点的光线在MP的角度从水面发生反射，沿着和MP相等的入射角SMP的角度从水面上发射出去。从△ADM、△A'DM两个三角形是全等三角形可以得知，∠SMP的角度要小于∠PMA的角度，这证明了星星S反射的光线并不在∠BA'C的范围内，而是从A点旁经过。如果星星S的光线被河水反射的地点离河岸的距离比M点离岸更近，那么反射光线与观察者的距离也更远。

我们分析到这里，你就可以知道果戈里对于星空的描写带有文学性的夸张成分，第聂伯河中的星星并不是天空中所有的星星，事实上，天空中的星星比映照河中的要多得多。而且更加出乎人意外的是，并不是越宽广的河流看到的星星就越多。在河岸低矮、河道狭窄的河岸边，你俯下身来，找到一个合适的角度，你会发现，你看到的星空更为广阔，正如图29中所示。你可以试着证明一下，会发现结果令你惊叹。

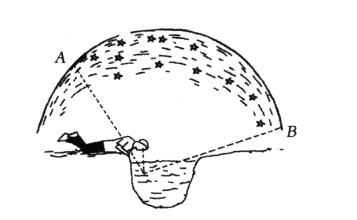
图29　在河岸低矮、河道狭窄的河中能够看见更多的星星