熟练掌握不同进数制相互之间的转换，在编写程序和设计数字逻辑电路时很有用，只要学会二进制数与十进制数之间的转换，二进制与八进制、十六进制数的转换就相对比较简单。

1）各种计数制之间的转换规律

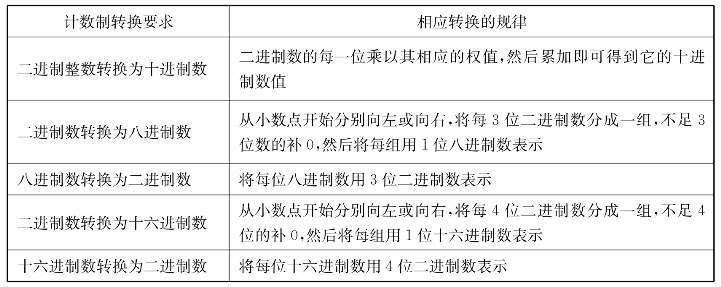
各种计数制之间的转换规律，如表1.4所示。

表1.4　各种计数制之间的转换规律

续表

2）数制转换举例

（1）二进制数与十进制数之间的互换。

①十进制数→二进制数。

例：29.6875→11101.1011B。

②二进制数→十进制数。

例：11101.1011B→29.6875。(www.daowen.com)

11101.1011B＝1×24＋1×23＋1×22＋0×21＋1×20整数部分

＝1×2－1＋0×2－2＋1×2－3＋1×2－4小数部分

＝29.6875

（2）二进制数与八进制数之间的互换。

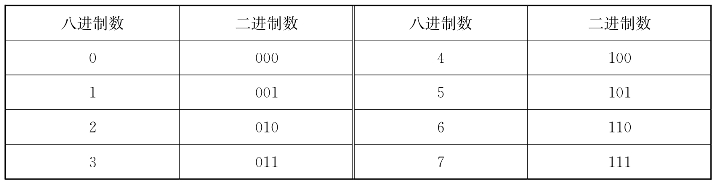
1位八进制数与3位二进制数的对应关系如表1.5所示。①二进制数→八进制数：整数部分从低位向高位每3位用一个等值的八进制数来替换，不足3位时在高位补0凑满3位；小数部分从高位向低位每3位用一个等值的八进制数来替换，不足3位时在低位补0凑满3位。

表1.5　1位八进制数与3位二进制数的对应关系

例：1101001110.11001B→001 101 001 110.110 010B→1516.62O。

②八进制数→二进制数：把每个八进制数字改写成等值的3位二进制数，且保持高低位的次序不变。

例：2467.32O→010 100 110 111.011 010B→10100110111.01101B。

（3）二进制数与十六进制数之间的互换。

转换方法与二进制数与八进制数之间的互换方法相似，对应取位个数由二进制数与八进制数互换时取的3位变成4位。