这是确定“单元格组”数字的方法，虽然我们不能确定哪一个数字具体在哪一个单元格中，但能确定这几个数字就是这几个单元格的数字。这样我们就可以把它当成已知数对待，为解题提供新的依据。

一、�如果在单元区（某一行、某一列或某一宫格）中出现以下情况

1 两个单元格：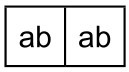

2 三个单元格：

3 四个单元格：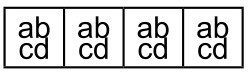

我们就可确定这几个单元格具有出现的全部数字，有了这些已知数，把它作为一个整体，再进一步推导出其他数字。

特别值得注意的是，在三个单元格项的B、C、D里，如果是在行或列的情况下，后面两个单元格还在一个宫格中，那这个宫格里一定有c。在隐性数字法里会使用这样的手段。

确定四个单元格组数字的方法，常在“宫”中应用，而且四个格子中某些格子的数字可能少1～2个，并不是全部4个，但在这组中应包括a、b、c、d四个数。

二、�如果在两行、两列四个交叉点出现下列情况，我们就可确定在这两行、这两列中存在c

图22

f列含数对a、c；

i列含数对b、c，则不但f列、i列含数字c，C行、F行也一定含数字c。

图23

C行含数对a、c；(www.daowen.com)

F行含数对b、c，则不但C行、F行含数字c，f列、i列也一定含数字c。

三、�如果在“偶数个”单元格中出现相同的数对，我们就可确定首、尾两个单元格一定含有这两个数字（即一个单元格是a，另一个单元格一定是b）

什么是偶数个单元格呢？如两个单元格，四个单元格，六个单元格……双数个单元格，即为偶数单元格。

什么是“首、尾单元格”呢？指在这类问题中，一个单元格数字确定，只引起另一个单元格数字确定。而不是能同时引起两个单元格数字确定。假如还不能理解这句话，你可以根据相关性把这些数字连接起来成一条折线，这条线两端的单元格即是“首、尾单元格”。

图24

四个单元格有相同的数对ab，D行两个单元格相关，h列两个单元格相关，VI宫两个单元格相关。

图25

把D行的两个单元格▲和△连接起来，把h列两个相关单元格●和○连接起来，把VI宫两个单元格△和●连接起来，就会看到是一条折线。这条线的首尾两端为▲和○（这两端互不相关）。则这两个单元格即为“首、尾单元格”。这样可以用排列法推导出★单元格数字。

图26

六个单元格有相同的数对ab，F行两个单元格相关，c列两个单元格相关，d列两个单元格相关，Ⅳ宫两个单元格相关，Ⅷ宫两个单元格相关。

图27

把F行的两个相关单元格■和□连接起来，把c列两个相关单元格▲和△连接起来，把d列两个相关单元格□和●连接起来，把Ⅳ宫两个相关单元格△和■连接起来，再把Ⅷ宫两个相关单元格●和○连接起来，就会看到是一条折线。这条线的首、尾两端为▲和○。它们每一个确定时，线的另一端数字会确定（只一个数字会确定）。而△、■、□、●这四个单元格，它们每一个确定时，会引起线两端数字都会确定（两个数字会确定）。