图形结构是一种比线性表和树形结构更复杂的非线性数据结构。线性结构中,数据元素之间具有单一的线性关系;树形结构中,节点间具有一对多的分支层次关系。在图形结构中,任意两个节点间可能有关系也可能根本不存在任何关系,节点间是多对多的复杂关系。可以说,树是图的特例,线性表是树的特例。

(1)图的定义和基本术语

1)图的特征

任意两个数据元素之间都可能相关。结点之间的关系是多对多的。

G=(V,E)

其中V是顶点的有限集合,记为V(G),E是连接V中两个不同顶点(即顶点对)的边的有限集合,记为E(G)。

2)基本术语

①结点:顶点。

②无向图:边(v,w),v与w互为邻接点,边(v,w)依附于顶点v、w,边(v,w)和顶点v、w相关联。

③v的度:和v相关联的边的数目。

④有向图:弧<v,w>,v弧尾,w弧头,顶点v邻接到顶点w,顶点w邻接自顶点v,弧<v,w>和顶点v,w相关联。

⑤v的入度:以v为头的弧的数目;v的出度:以v为尾的弧的数目。

⑥v的度:v的入度与出度之和。

⑦路径、回路(环)、简单路径、简单回路(简单环)

⑧连通性:若从顶点v到顶点v′有路径,则称v和v′是连通的。

⑨图的规模:顶点数n、边(弧)数e、顶点的度(有向图:入度/出度)。

⑩子图:G′=(V′,{E′}),G=(V,{E}),若V′⊆V且E′⊆E,则称G′是G的子图。

3)图的分类

①关系的方向性(无向/有向)、关系上是否有附加的数——权(图/网)有向图、无向图、有向网、无向网。

②边(弧)数:完全图[边数=n(n-1)/2的无向图]、有向完全图[弧数=n(n-1)的有向图]、稀疏图(e<n log n)、稠密图(e>n log n)。

③连通性:无向图、连通图(任意两顶点都是连通的)、连通分量(极大连通子图)、生成树(极小连通子图)、生成森林。

④有向图:强/弱连通图、强连通分量、生成树(极小连通子图)、生成森林。

(2)图的存储与操作

图的存储结构相比较线性表与树来说就复杂很多。对于线性表来说,是一对一的关系,所以用数组或者链表均可简单存放。树结构是一对多的关系,所以我们要将数组和链表的特性结合在一起才能更好地存放。那么我们的图,是多对多的情况,另外图上的任何一个顶点都可以被看成第一个顶点,任一顶点的邻接点之间也不存在次序关系。(www.daowen.com)

因为任意两个顶点之间都可能存在联系,因此无法以数据元素在内存中的物理位置来表示元素之间的关系(内存物理位置是线性的,图的元素关系是平面的)。如果用多重链表来描述倒是可以做到,但在几节课前的树章节我们已经讨论过,纯粹用多重链表导致的浪费是无法想象的(如果各个顶点的度数相差太大,就会造成巨大的浪费)。

1)邻接矩阵

邻接矩阵(adjacencymatrix)是表示顶点之间相邻关系的矩阵。设G=(V,E)是一个图,其中V={v1,v2,…,vn}。G的邻接矩阵是一个具有下列性质的n阶方阵:

①对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),副对角线不一定为0,有向图则不一定如此。

②在无向图中,任一顶点i的度为第i列(或第i行)所有非零元素的个数,在有向图中顶点i的出度为第i行所有非零元素的个数,而入度为第i列所有非零元素的个数。

③用邻接矩阵法表示图共需要n2个空间,由于无向图的邻接矩阵一定具有对称关系,所以扣除对角线为零外,仅需要存储上三角形或下三角形的数据即可,因此仅需要n(n-1)/2个空间。

邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。可以设置两个数组,顶点数组为vertex[4]={v0,v1,v2,v3},边数组arc[4][4]为对称矩阵(0表示不存在顶点间的边,1表示顶点间存在边),如图6.44所示。

2)邻接表

对于边数相对顶点较少的图,这种结构无疑是存在对存储空间的极大浪费。因此可以考虑另一种存储结构方式,例如把数组与链表结合到一起来存储,这种方式在图结构也适用,称为邻接表,如图6.45所示。

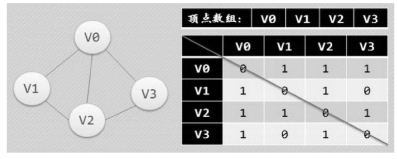
图6.44　无向图邻接矩阵

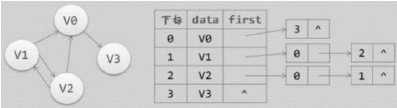
图6.45　有向图邻接表

图的邻接表存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。如词条概念图所示,表结点存放的是邻接顶点在数组中的索引。对于无向图来说,使用邻接表进行存储也会出现数据冗余,表头结点A所指链表中存在一个指向C的表结点的同时,表头结点C所指链表也会存在一个指向A的表结点。

邻接表是图的一种最主要存储结构,用来描述图上的每一个点。对图的每个顶点建立一个容器(n个顶点建立n个容器),第i个容器中的结点包含顶点Vi的所有邻接顶点。实际上我们常用的邻接矩阵就是一种未离散化每个点的边集的邻接表。

在有向图中,描述每个点向别的节点连的边(点a→点b这种情况)。在无向图中,描述每个点所有的边(点a→点b这种情况)。与邻接表相对应的存图方式叫作边集表,这种方法用一个容器存储所有的边。

3)十字链表

十字链表(orthogonal list)是有向图的另一种链式存储结构。可以看成将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中,对应于有向图中每一条弧都有一个结点,对应于每个定顶点也有一个结点。

十字链表之于有向图,类似于邻接表之于无向图。也可以理解为:将行的单链表和列的单链表结合起来存储稀疏矩阵称为十字链表,每个节点表示一个非零元素,如图6.46所示。

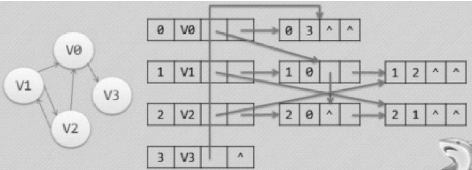
图6.46　有向图十字链表

注意

邻接矩阵适用于表示稠密图,邻接表适用于表示稀疏图;邻接表求有向图的顶点的入度不方便,要遍历全部的邻接表。