树形结构指的是数据元素之间存在着“一对多”的树形关系的数据结构,是一类重要的非线性数据结构。在树形结构中,树根结点没有前驱结点,其余每个结点有且只有一个前驱结点。叶子结点没有后续结点,其余每个结点的后续节点数可以是一个也可以是多个。

(1)树的基本术语

①树结点(tree node):树中一个独立单元。包含一个数据元素及若干指向其子树的分支,图6.40中的A,B,C,D等。

②树根(root):树中唯一没有前驱的结点,图6.40中的A结点。

③结点的度(node degree):结点拥有的子树数,称为结点的度。例如,图6.40中A的度为3,B的度为2,K的度为0。

④树的度(tree degree):树中各结点的度的最大值,图6.40中树的度为3。

⑤树叶(leaf):度为0的结点。例如,在图6.40中,K,L,F,G,I,J,M都是树叶,也称叶结点。除根和叶子以外的其他结点称为中间结点。

⑥双亲(parent)和孩子(child):把一个树结点的直接前驱称为该结点的双亲;反之,把一个树结点的所有直接后继称为该结点的孩子。例如,图6.40中,结点B是结点A的孩子,结点A是结点B的双亲。

⑦兄弟(sibling):同一双亲的孩子之间互称为兄弟。例如,图6.40中,结点K,L互为兄弟,结点H,I,J互为兄弟。将这些关系进一步推广,结点的祖先就是从根到该结点的所经分支上的所有结点。以某结点为根的子树中的任一结点都称为该结点的子孙。此外双亲在同一层上的结点互为堂兄弟。

⑧树的层次(level)和深度(depth):从根算起,根为第一层,根的孩子为第二层,树中任一结点的层次等于它的双亲的层次加1。树中各结点层次的最大值称为树的深度或高度。例如,上图中的树的深度为4。

⑨有序树和无序树(ordered tree,unordered tree):如果树中结点的各子树可看成从左至右是有次序的(即不能互换),则称该树为有序树,否则称为无序树。在有序树最左边子树的根称为第一孩子,最右边子树的根称为最后一个孩子。

⑩森林(forest):m(m≥0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。由此也可以以森林和树的相互递归定义来描述树。

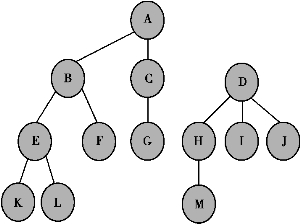
图6.40　树形结构

(2)树的存储结构

树是一种非线性结构。为了存储一棵树,必须把树中各结点之间一对多的关系反映在存储结构中。由于在一个m阶的普通树中,每一个结点的孩子有0～m个,所以相对于二叉树而言,树的存储结构更复杂,一般有如下几种存储结构:(www.daowen.com)

1)双亲表示法

让每个结点记住其父结点的位置。存储数据元素的结点由两部分组成:存储数据元素值的数据字段,以及存储父结点位置的父指针字段。树的所有结点可存放在一个数组中(称“静态双亲表示法”),也可组织成一个链表(称“动态双亲表示法”)。

当算法中需要在树结构中频繁地查找某结点的父结点时,使用双亲表示法最合适。当频繁地访问结点的孩子结点时,双亲表示法就很麻烦,采用孩子表示法就很简单,如图6.41所示。

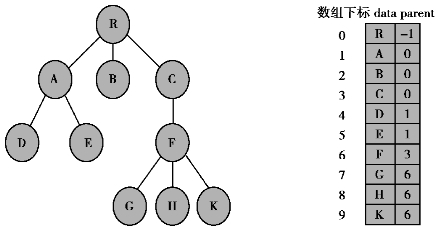
图6.41　双亲表示法

2)孩子表示法

孩子表示法是树的一种存储方式,其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。如果节点没有孩子节点(叶子节点),则该节点的链表为空链表,如图6.42所示。

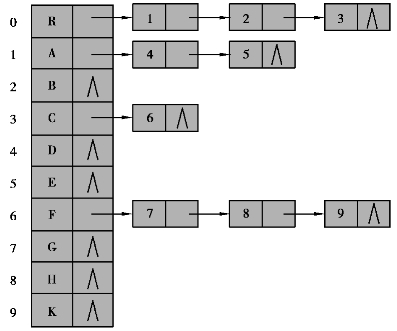
图6.42　孩子表示法

图6.43　结点构成

3)孩子兄弟表示法

使用链式存储结构存储普通树。链表中每个结点由3部分组成,如图6.43所示。

其中孩子指针域,表示指向当前结点的第一个孩子结点,兄弟结点表示指向当前结点的下一个兄弟结点。