计算机除了用于数值数据计算之外,还要进行大量的数字和字符数据的处理,但各种信息都是要以二进制编码的形式存在的,因此,计算机处理时要对数字和字符进行二进制编码。

(1)数字的编码

在将十进制数输入计算机时,计算机应马上将其转换为二进制数,但是在将所有位的数字输入之前又不可能知道它到底是在百位还是其他位上,因此也就不可能转换得到对应的二进制数,为此人们引入了数字的二进制编码。因此,在计算机输入数字或者输出数字时,都要进行二进制与十进制的相互转换。用于表示十进制数的二进制代码称为二十进制编码(Binary Coded Decimal,BCD)。

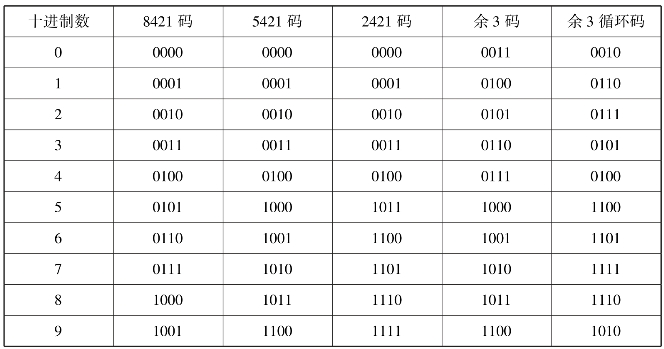
BCD码是二进制编码形式表示的十进制数,它既具有二进制数的形式,可以满足数字系统的要求,又具有十进制的特点。BCD码的编码方法很多,可分为有权码和无权码两类,常见的有权BCD码有8421码、5421码、2421码,无权BCD码有余3码、余3循环码、格雷码。常见的BCD码见表4.6。

表4.6　常见的BCD编码

1)8421码

8421码是最基本和最常用的BCD码,是一种有权码。其编码的方法是用4位二进制数表示1位十进制数,自左至右每一位对应的位权分别是8,4,2,1,故称为8421码。4位二进制数有0000～1111共16种状态,而十进制数只有0～9共10个数码,8421码只取0000～1001共计10种状态。由于8421码应用最广泛,所以一般说BCD码就是指8421码。

设8421码的各位为A3,A2,A1,A0,则它所代表的值为

X=8A3﹢4A2﹢2A1﹢A0

8421码编码简单直观,可以容易地实现8421码与十进制数之间的转换。

例4.23　将十进制数10.54转换为8421码。

8421码表示为

(10.54)10=(0001 0000.0101 0100)8421

例4.24　写出十进制数7852的8421码。

8421码为0111　1000　0101　0010,实际存储时可以占用4字节(每个字节的高4位补成0000),称为非压缩BCD码,也可用2字节存储,称为压缩BCD码。

2)5421码

5421码由权5,4,2,1的4位二进制数组成,它也是一种有权码,其代表的十进制数可由下式算得:

X=5A3﹢4A2﹢2A1﹢A0

其中A3,A2,A1和A0为5421码的个位数(0或1)。对同一个十进制数,5421码可能有多种编码方法。

3)2421码

2421码由权2,4,2,1的4位二进制数组成,2421码的特点与8421码相似,它也是一种有权码,其代表的十进制数可由下式算得:

X=2A3﹢4A2﹢2A1﹢A0

其中A3,A2,A1和A0为2421码的个位数(0或1)。与8421码不同的是,对同一个十进制数,2421码可能有多种编码方法,2421编码见表4.7。

表4.7　2421编码

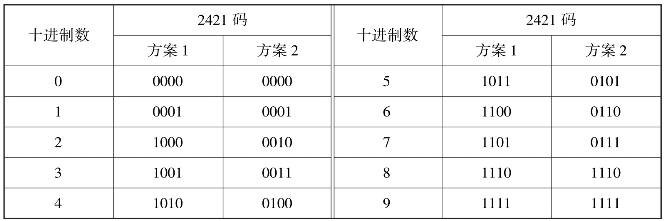
表4.7中的两种2421码都只用了4位二进制数16种组合中的10种,方案1在十进制数1和2之间跳过6种组合,而方案2在十进制数7和8之间跳过6种组合。

需要指出的是,表4.6中第三列所给出的2421码是一种自反编码,或称对9的自补码,只要把这种2421码的各位取反,便可得到另一种2421码,而且这两种2421码所代表的十进制数对9互反,例如,2421码0100代表十进制数4,若将它的各位取反得1011,它所代表的十进制数5恰是4对9的反。必须注意,并不是所有的2421码都是自反代码。

4)余3码

十进制数的余3码是由对应的8421码加0011后得到的,故称为余3码。显然,余3码A3,A2,A1,A0所代表的十进制数可由下式算得:

X=8A3﹢4A2﹢2A1﹢A0-3

余3码是一种无权代码,该代码中的各位1不是一个固定值,因而不直观。余3码也是一种自反代码。由表4.6可知,4的余3码为0111,将它的各位取反得1000,即5的余3码,而4与5对9互反。

另一个特点:两个余3码相加时,所产生的进位相当于十进制数的进位,但对“和”必须进行修正。修正的方法:如果产生进位,则留下的和为8421码,需加上0011加以修正;如果不产生进位,则加上1101(13)[或减去0011(3)],即得和数的余3码,最终的进位要看修正时的进位。

例4.25　余3码0101与0110相加。

相加后的结果不产生进位,加1101进行修正,因此(0101)余3码﹢(0110)余3码=(1000)余3码。

例4.26　余3码0110与1100相加。

最终结果为0101,进位为1。

5)格雷码

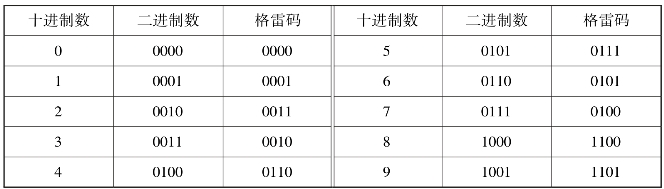
格雷码(也称循环码)是由贝尔实验室的Frank Gray在1940年提出的,用于PCM(Pusle Code Modulation)方法传送信号时防止出错。格雷码是一个数列集合,它是无权码,它的两个相邻代码之间仅有一位取值不同。典型格雷码是一种具有反射特性和循环特性的单步自补码,它的循环、单步特性消除了随机取数时出现重大误差的可能,它的反射、自补特性使得求反非常方便。格雷码属于可靠性编码,是一种错误最小化的编码方式。编码方法见表4.8。

表4.8　格雷码

续表

(www.daowen.com)

①二进制码转换成格雷码

二进制码的最高位作为格雷码的最高位,次高位格雷码为二进制码的最高位与次高位相异或,格雷码的其余各位依次类推。设n位二进制码为

Bn-1 Bn-2…B2 B1 B0

对应的n位格雷码为

Gn-1Gn-2…G2G1G0

则格雷码的最高位保留二进制码的最高位

Gn-1=Bn-1

其他各位为

Gi=Bi﹢1⊕Bi,i=0,1,2,…,n-2

例4.27　将二进制数10110转换为格雷码。

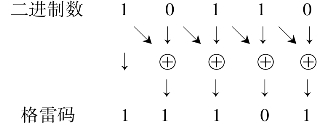
所以:(10110)2=(11101)格雷码

②格雷码转换成二进制码

格雷码的最高位作为二进制码的最高位,次高位二进制码为二进制码的最高位与格雷码次高位相异或,二进制码的其余各位依次类推。设n位格雷码为

Gn-1Gn-2…G2G1G0

对应的n位二进制码为

Bn-1 Bn-2…B2 B1 B0

则二进制码的最高位保留格雷码的最高位

Bn-1=Gn-1

其他各位为

Bi-1=Gi-1⊕Bi,i=0,1,2,…,n-1

例4.28　将格雷码10110转换为二进制数。

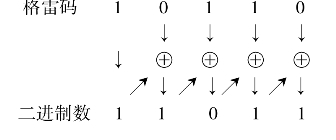
所以:(10110)格雷码=(11011)2

6)余3循环码

余3循环码是变权码,每一位的1并不代表固定的数值。十进制数的余3循环码就是取4位格雷码中的10个代码组成的,即从0010到1010(表4.6),具有格雷码的优点,即两个相邻代码之间仅有一位的状态不同。

(2)字符编码

计算机中的非数值信息也采用0和1两个符号的编码来表示。

1)ASCII码

目前,微型计算机中普遍采用的英文字符编码是ASCII码(American Standard Code for Information Interchange,美国国家标准信息交换码)。它采用一个字节来表示一个字符,在这个字节中,最高位为0(零),低7位为字符编码,00000000～01111111(0～127)共代表了128个字符,标准7位ASCII码字符集见表4.9。

表4.9　标准7位ASCII码字符集

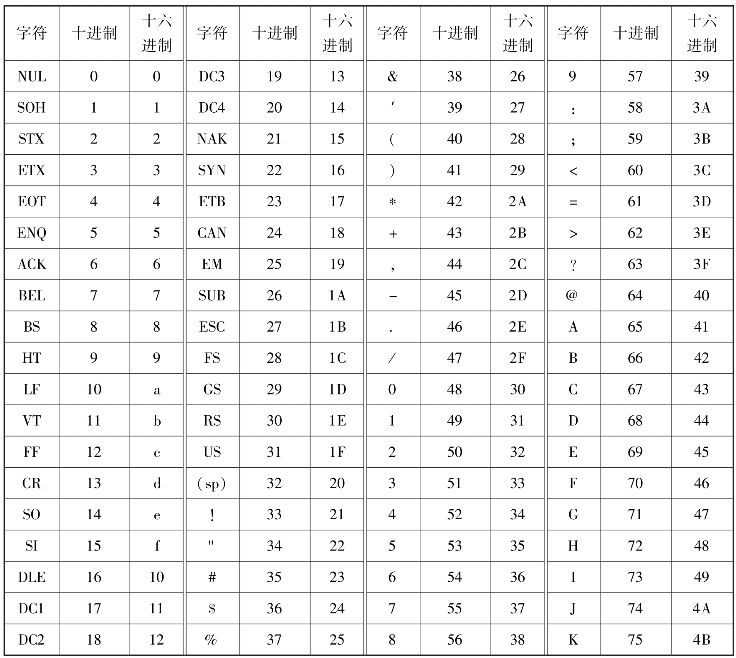
续表

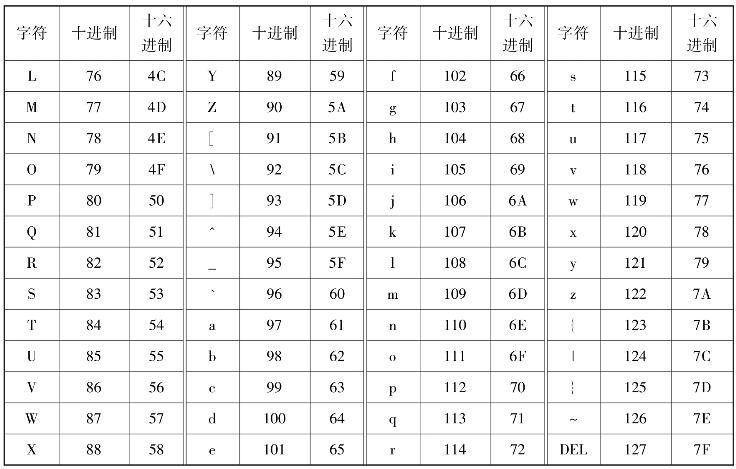
在这128个ASCII码字符中,编码0～31是32个不可打印和显示的控制字符,其余96个编码则对应着键盘上的字符。除编码32和128这两个字符不能显示出来之外,另外94个字符均为可以显示。从表4.9中可以看出以下规律:

①数字0的ASCII码是48 D或30 H;大写字母A的ASCII码是65 D或41 H;小写字母a的ASCII码是97 D或61 H。

②数字0～9、大写字母A～Z、小写字母a～z的ASCII码值是连续的。因此,如果知道了数字0、大写字母A和小写字母a的ASCII码值,就可以推算出所有数字和字母的ASCII码值。例如,A的ASCII码为1000001,对应的十进制数是65,由A～Z编码连续可以推算出字母D的ASCII码是68(十进制数)。

③数字0～9的ASCII码值小于所有字母的ASCII码值;大写字母的ASCII码值小于小写字母的ASCII码值;大写字母与其对应的小写字母之间的ASCII码值之差正好是十进制数32。

例4.29　写出英文单词Computer的ASCII码。

ASCII码的二进制形式:01000011　0110111　01101101　01110000　01110101 01110100　01100101　01110010,写成十六进制形式:43　6F　6D　70　75　74　65　72。

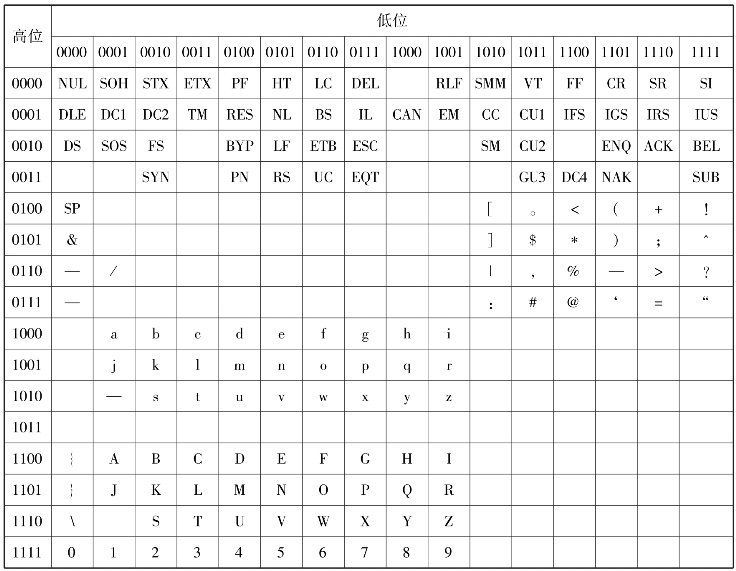
2)EBCDIC码

EBCDIC(Extended Binary Coded Decimal Interchange Code)码即扩展的BCD码,是IBM公司于1963—1964年间推出的字符编码表,除了原有的10个数字之外,又增加了一些特殊符号、大小写英文字母和某些控制字符的表示,也是一种字符编码。采用8位二进制编码来表示一个字符或数字字符,共可以表示256个不同符号,EBCDIC中只选用了其中一部分,其他的用作扩充。EBCDIC码见表4.10,主要用于超级计算机和大型计算机。其缺点是英文字母不是连续地排列,中间出现多次断续,为撰写程序的人带来了一些困难。

表4.10　EBCDIC码