数值数据既有正数和负数之分,又有整数和小数之分。在计算机中,对于数值数据小数点的表示方法,有定点表示法和浮点表示法,定点表示法小数点的位置是固定不变的,浮点表示法小数点的位置是浮动变化的。

(1)定点表示法

在计算机内部结构中指定一个不变的位置作为小数点的位置。常用的有定点整数和定点小数两种格式。

定点整数表示法是将小数点的位置固定在表示数值的最低位之后,其一般格式如图4.1所示。定点整数表示法只能表示整数,运算时则要求参加运算的数都是整数。如果参加运算的数是小数,则在计算机表示之前需乘以一个比例因子,将其放大为整数。

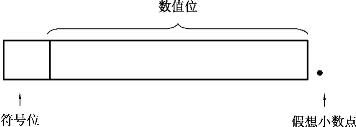
图4.1　定点整数表示法的一般格式

定点小数表示法是将小数点的位置固定在符号位和数值位之间,其一般格式如图4.2所示。定点小数表示法只能表示纯小数(绝对值小于1的小数),运算时则要求参加运算的数都是纯小数。如果参加运算的数是整数或绝对值大于1的小数,则在计算机表示之前需乘以一个比例因子,将其缩小为纯小数。

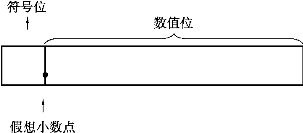
图4.2　定点小数表示法的一般格式

对于定点表示法,由于小数点始终固定在一个确定的位置,所以计算机不必将参加运算的数对齐即可直接进行加减运算。当参与运算的数值数据本身就是定点数形式时,计算简单方便。但是,定点表示法需要对参加运算的数进行比例因子的计算,因而增加了额外的计算量。

(2)浮点表示法

在科学计算和数据处理中,经常需要处理非常大的数或非常小的数。在计算机的高级语言设计中,通常采用浮点方式表示实数,一个实数X的浮点形式(即科学计数法)表示为

X=M×RE(www.daowen.com)

其中,R表示基数,由于计算机采用二进制,所以基数R=2。E为R的幂,称为数X的阶码,其值确定了数X的小数点位置。M为数X的有效数字,称为数X的尾数,其位数反映了数据的精度。

从上式中可以看出,尾数M中的小数点可以随E值的变化而左右浮动,因此这种表示法称为浮点表示法。目前大多数计算机多把尾数M规定为纯小数,把阶码E规定为整数。

一旦计算机定义了基数就不能再改变了,因此浮点表示法无须表示基数。计算机中浮点数的表示由阶码和尾数两部分组成,其中阶码一般用定点整数表示,尾数用定点小数表示。浮点表示法的一般格式如图4.3所示。

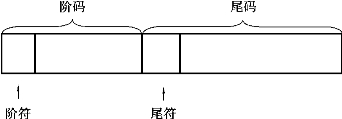
图4.3　浮点表示法的一般格式

例4.16　设X=3.625,假设用12位二进制数表示一个浮点数,其中阶码占4位,尾数占8位,则其浮点表示为

(3.625)10=(11.101)2=0.11101×210

阶码为﹢10,其补码为010,则阶码表示为0010,尾数为﹢0.11101,其补码为011101,占8位,则尾数表示为01110100。因此X的浮点数表示为:001001110100。

例4.17　设X=3.625,假设用8位二进制数表示一个浮点数,其中阶码占3位,尾数占5位,则其浮点表示为

(3.625)10=(11.101)2=0.11101×210

阶码为﹢10,其补码为010,尾数为﹢0.11101,其补码为011101,由于尾数占5位,位数不够,则尾数表示为01110。因此X的浮点数表示为:001001110。实际上001001110是3.5的浮点表示,由于尾数的空间不够大,从而产生了截断误差,若要保证数据有足够的精度,则尾数要有足够的位数。