计算机中表示一个整数数据,需考虑整数的长度及正负号的表示。

在计算机中,数的长度是指该数所占的二进制位数,由于存储单元通常以字节为单位,因此,数的长度也指该数所占的字节数。同类型的数据长度一般是固定的,由机器的字长确定,不足部分用0补足,即同一类型的数据具有相同的长度,与数据的实际长度无关。例如,某16位计算机,其整数占两个字节(即16位二进制),所有整数的长度都是16位,则(68)10=(1000100)2=(00000000 01000100)2。

整数数据有正数和负数之分,由于计算机中使用二进制0和1,因此,可以采用一位二进制表示整数的符号,通常用“0”表示正号,用“1”表示负号,即对符号位也可进行编码。

在以下讨论中,假设用8位二进制数表示一个整数,用X表示数的真值,用[X]原、[X]反、[X]补分别表示原码、反码和补码。

(1)数的原码、反码和补码

1)原码

原码是一种最简单的表示方法。其编码规则:数的符号用一位二进数表示(称为符号位),与数的绝对值一起编码。

例4.10　设带符号数的真值X=﹢69和Y=-69,则它们的原码分别为

[X]原=01000101　[Y]原=11000101

原码表示法虽然简单直接,但也存在缺点。

①零的表示不唯一。由于[﹢0]原=00000000,[-0]原=10000000,从而给机器判零带来困难。

②进行四则运算时,符号位需单独处理。例如加法运算,若两数同号,则两数相加,结果取共同的符号;若两数异号,则用大数减去小数,结果取大数的符号。

③硬件实现困难。如减法需要单独的逻辑电路来实现。

2)反码

反码不常用,是求补码的中间码,其编码规则:正数的反码与原码相同,负数的反码其符号位与原码相同,其余各位取反。

例4.11　设带符号数的真值X=﹢69和Y=-69,则它们的原码和反码分别为

[X]原=01000101　[X]反=01000101

[Y]原=11000101　[Y]反=10111010

3)补码

补码是一种使用最广泛的表示方法,其理论基础是模数的概念。例如,钟表的模数为12,如果现在的准确时间是3点,而你的手表显示时间是8点,怎样把手表拨准呢?可以有两种方法:一种是把时针往后拨5小时;另一种是往前拨7小时。之所以这两种方法效果相同,是因为5和7对模数12互为补数。即一个数A减去另一个数B,等价于A加上B的补数。

补码的编码规则:正数的补码与原码相同,负数的补码其符号位与原码相同,其余各位取反再在最末位加1(取反加1)。PC采用补码存储数据,因此CPU只需有加法器即可。

例4.12　设带符号数的真值X=﹢69和Y=-69,则它们的原码和补码分别为:

[X]原=01000101　[X]反=01000101

[Y]原=11000101　[Y]反=10111011

由于[﹢0]补=00000000,[-0]补=[-0]反﹢1=11111111﹢1=00000000,因此,补码表示的优点之一就是零的表示唯一。

例4.13　[﹢127]补=01111111,[-127]补=10000001,[-128]补=10000000

(2)定点整数(www.daowen.com)

定点整数的小数点默认为在二进制数最后一位的后面。在计算机中,正整数是以原码(即二进制代码本身)的形式存储的,负整数则是以补码的形式存储的。由于正整数的补码与原码相同,所以无论是正整数还是负整数,都是以补码的形式存储的。

用补码表示整数运算时不需要单独处理符号位,符号位可以像数值一样参与运算。

补码的加法:[X﹢Y]补=[X]补﹢[Y]补

补码的减法:[X-Y]补=[X]补-[Y]补=[X]补﹢[-Y]补

补码的乘法:[X×Y]补=[X]补×[Y]补

例4.14　计算68-12的值。

解:68=﹢1000100　[68]补=01000100

-12=-0001100　[-12]补=[-12]反﹢1=11110011﹢1=11110100

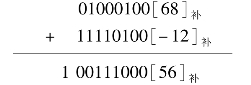
例4.15　计算12-68的值。

解:12=﹢0001100　[12]补=00001100

-68=-1000100　[-68]补=[-68]反﹢1=10111011﹢1=10111100

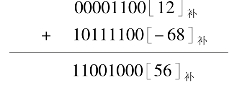
补码运算的结果仍为补码,再将补码转换回原码,即可得到运算的结果,如例4.15的运算结果为56(因为结果为正数,故补码就是原码)。如果运算结果为负数,可以用减1再取反(符号位不变)的逆过程求出原码。

(3)无符号整数

无符号数是指在字节、字或双字整数操作数中,对应的8位、16位或32位二进制数全部用来表示数值本身,无表示符号的位,因而是正整数。

若机器字长为n,则无符号整数数值范围为0～(2n-1),无符号(unsigned)整数的类型,取值范围如表4.3所示。

在计算机中无符号整数常用于表示地址数。

表4.3　无符号整数类型取值范围

(4)带符号整数

在计算机数据处理中,除了无符号整数外,还有4种带符号数,带符号数的表示方法是把二进制的最高位定义为符号位,其余各位表示数值本身。占有n个二进制位的带符号数的取值范围是-2n-1～2n-1-1,表4.4表示不同整数类型所占的字节数及可表示的范围。

表4.4　4种带符号类型整数

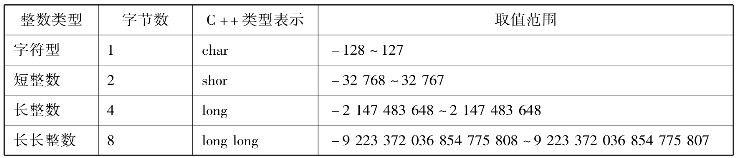
有符号数在计算机中以补码的形式存储,无符号数其实就是正数,存储形式是十进制真值对应的二进制数,所以无论是有符号数还是无符号数,都是以补码(相对真值而言)的形式存储的,补码在运算时符号位也会参与。