(1)将R进制数转换为十进制数

将一个R进制数转换为十进制数的方法是先按权位展开,再按十进制运算法则依次相加。

例4.1　将二进制数(101101.101)2转换为十进制数。

(101101.101)2=1×25﹢0×24﹢1×23﹢1×22﹢0×21﹢1×20﹢1×2-1﹢0×2-2﹢1×2-3=(45.625)10

例4.2　将八进制数(23.4)8转换为十进制数。

(23.4)8=2×81﹢3×80﹢4×8-1=(19.5)10

例4.3　将十六进制数(1D9.4)16转换为十进制数。

(1D9.4)16=1×162﹢13×161﹢9×160﹢4×16-1=(473.25)10

(2)将十进制数转换为R进制数

将十进制数转换为等值的二进制数、八进制数和十六进制数的方法是分别对整数部分和小数部分进行转换。

整数部分(基数除法):连续除以基数R,直到商为0为止,再将每次得到的余数按逆序排列,即为R进制数的整数部分。

小数部分(基数乘法):连续乘基数R,直到积为整数为止,再将得到的整数部分按顺序排列,即为R进制数的小数部分。

例4.4　将十进制数(100.6875)10转换为二进制数。

即(100.6875)10=(1100100.1011)2。

例4.5　将十进制数(100)10分别转换为八进制数和十六进制数。

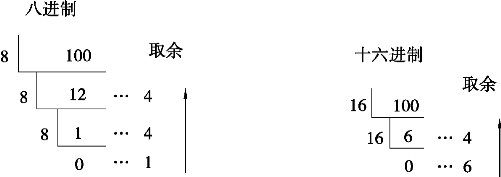
即(100)10=(144)8=(64)16。

(3)二进制数、八进制数、十六进制数的相互转换(www.daowen.com)

二进制数、八进制数和十六进制数之间的相互转换很有实用价值。由于这3种进制的权之间存在内在联系,即23=8,24=16,因而它们之间的转换比较容易,即每位八进制数相当于3位二进制数,每位十六进制数相当于4位二进制数。

表4.1　二进制数与八进制数转换表

表4.2　二进制数与十六进制数转换表

在转换时,位组划分是以小数点为中心向左右两边进行的,中间的0不能省略,两头不足时可以补0。

例4.6　将二进制数(11010.110101)2分别转换为八进制数和十六进制数。

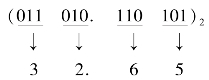
即(11010.110101)2=(32.65)8。

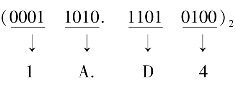
即(11010.110101)2=(1A.D4)16。

例4.7　将八进制数(714.65)8转换为二进制数。

即(714.65)8=(111001100.110101)2。

例4.8　将十六进制数(C2B.5F)16转换为二进制数

即(C2B.5F)16=(110000101011.01011111)2。

如果要将八进制数转换成等值的十六进制数,可以先将八进制数转换成二进制数,再把二进制数转换成十六进制数,反之亦然。例如,(32)8=(11010)2=(1A)16。