数制是指用一组固定的符号和统一的规则来表示数值的方法。其中，按照进位方式计数的数制称为进位计数制。在日常生活中，人们习惯用的进位计数制是十进制，而计算机则使用二进制；除此以外，还包括八进制和十六进制等。顾名思义，二进制就是逢二进一的数字表示方法；依次类推，十进制就是逢十进一；八进制就是逢八进一等。

进位计数制中每个数码的数值不仅取决于数码本身，其数值的大小还取决于该数码在数中的位置，如十进制数878.64，整数部分的第1个数码“8”处在百位，表示800，第2个数码“7”处在十位，表示70，第3个数码“8“处在个位，表示8，小数点后第1个数码“6”处在十分位，表示0.6，小数点后第2个数码“4”处在百分位，表示0.04。也就是说，同一数码处在不同位置所代表的数值是不同的，数码在一个数中的位置称为数制的数位；数制中数码的个数称为数制的基数，十进制数有0、1、2、3、4、5、6、7、8、9共10个数码，其基数为10；在每个数位上的数码符号所代表的数值等于该数位上的数码乘以一个固定值，该固定值称为数制的位权数，数码所在的数位不同，其位权数也有所不同。

无论在何种进位计数制中，数值都可写成按位权展开的形式，如十进制数878.64可写成：

878.64＝8×100＋7×10＋8×1＋6×0.1＋4×0.01

或者

878.64＝8×102＋7×101＋8×100＋6×10－1＋4×10－2

上式为数值按位权展开的表达式，其中10称为十进制数的位权数，其基数为10，使用不同的基数，便可得到不同的进位计数制。设R表示基数，则称为R进制，使用R个基本的数码，R就是位权，其加法运算规则是“逢R进一”，则任意一个R进制数D均可以展开表示为：

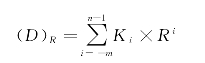(www.daowen.com)

式中，Ki为第i位的系数，可以为0，1，2…，R－1中的任何一个数，Ri表示第i位的权。

（注意：二进制数101B读为“一零一”或“幺零幺”，不能读作“一百零一”。）表1-1所示为计算机中常用的几种进位计数制的表示。

表1-1　计算机中常用的几种进位计数制

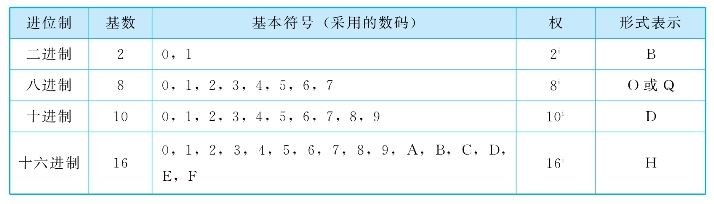
通过表1-1可知，对于数据3A8D，从使用的数码可以判断出其为十六进制数，而对于数据273来说，如何判断它属于哪种数制呢？在计算机中，为了区分不同进制的数，可以用括号加数制基数下标的方式来表示不同数制的数，例如，（376）10表示十进制数，（1011.1）2表示二进制数，（3A8D）16表示十六进制数，也可以用带有字母的形式分别表示为376D、1011.1B、3A8DH。

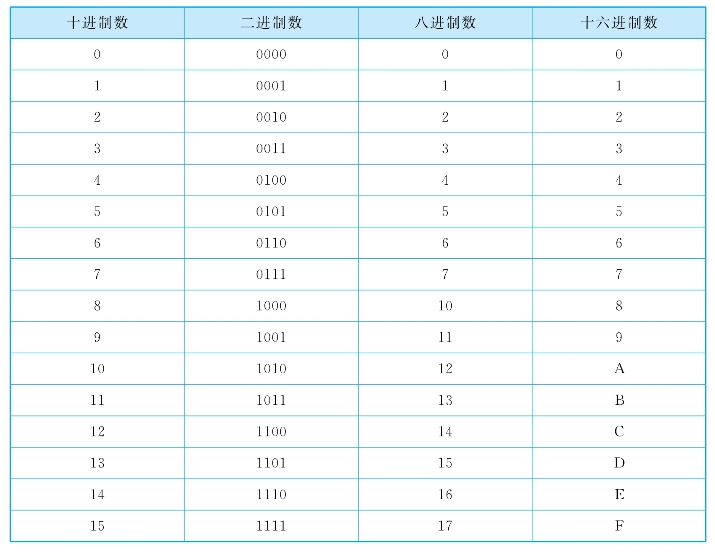
表1-2　常用数制对照关系表