Flac3D（Three Dimensional Fast Lagrangian Analysis of Continua）是由美国Itasca Consulting Group Inc开发的三维显式有限差分法程序，它可以模拟岩土或其他材料的三维力学行为。无论是动力问题，还是静力问题，Flac3D程序均由运动方程用显式方法进行求解，这使得它很容易模拟动力问题，如振动、失稳、大变形等。对显式法来说，非线性本构关系与线性本构关系并无算法上的差别，对于已知的应变增量，可很方便地求出应力增量，并得到不平衡力，就同实际中的物理过程一样，可以跟踪系统的演化过程。在计算过程中，程序能随意中断与进行，随意改变计算参数与边界条件。因此，较适合处理复杂的非线性岩土体开挖卸荷效应和流变问题［84－87］。

Flac3D的特点：

（1）不形成刚度矩阵，计算所需的内存小，适合在微机上操作。

（2）可以模拟复杂的岩土工程或力学问题，它包含了10种弹塑性材料本构模型，有静力、动力、蠕变、渗流、温度5种计算模式，各种模式间可以互相耦合，以模拟各种复杂的工程力学行为。

（3）具有强大的内嵌式语言FISH，使得用户可以自定义新的变量和函数，以适应用户的特殊需要；将开挖步信息写成FISH可以很容易地实现开挖步之间的批处理计算。

（4）Flac3D可以进行自定义跟踪，一旦不收敛现象出现，将很容易找出不收敛原因（非数值方法内部原因）。

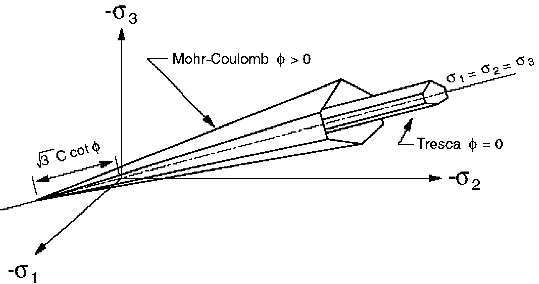
图5－1　主应力空间下摩尔－库仑和Tresca屈服面

它的主要缺点在于它前处理建模的不直观性，因此无法实现大型复杂岩体工程的建模和自动网格剖分，因为它并不采用实体建模，而采用程序内部存贮实体形式进行模型拼砌。工程中岩土体破坏一般遵循摩尔－库仑准则，故建议采用摩尔－库仑模型来衡量岩土体在极限平衡条件下的破坏条件，如图5－1至图5－2所示。

强度折减法是基于摩尔－库仑准则发展而来的一种采用数值仿真技术定量计算岩土体稳定性的分析方法。其定义为：在外荷载保持不变的情况下，边坡内岩土体所发挥的最大抗剪强度与外荷载在边坡内所产生的实际剪应力之比。这里定义的抗剪强度折减系数，与极限平衡分析中所定义的土坡稳定性系数在本质上是一致的。

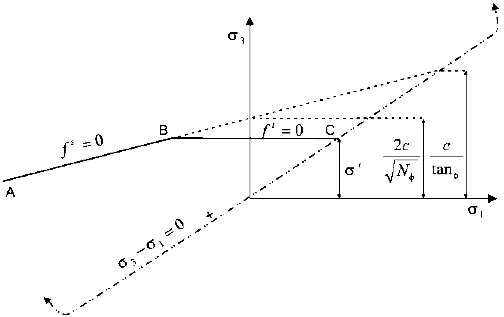
图5－2　Flac3D摩尔－库仑屈服准则

将岩土体的抗剪强度指标内聚力C和内摩擦角φ，同时用一个折减系数Fs，如式（5－1）和（5－2）所示的形式进行折减，然后用折减后的虚拟抗剪强度指标CF和φF，取代原来的抗剪强度指标C和φ［1］，如式（5－3）所示。(www.daowen.com)

式中：CF是折减后土体虚拟的粘聚力；φF是折减后土体虚拟的内摩擦角；tF是折减后的抗剪强度。折减系数Fs的初始值取得足够小，以保证开始时是一个近乎弹性的问题。然后不断增加Fs的值，折减后的抗剪强度指标逐步减小，直到某一个折减抗剪强度下整个边坡发生失稳，那么在发生整体失稳之前（“临界破坏状态”）的那个折减系数值，即土体的实际抗剪强度指标与发生虚拟破坏时折减强度指标的比值，就是这个边坡的稳定系数Fs（强度贮备安全系数）。

有关学者的研究结果表明：强度折减法不仅能够简单、准确地确定边坡安全系数，而且还可以通过相关的计算结果图得到边坡的潜在破坏位置，因此在边坡工程中有广泛应用。

通过SOLVE fos命令执行强度折减的程序步骤如下：

（1）将黏聚力c设置成大值，使内部应力发生变化，找到体系达到平衡的典型步数，记作Nr，Nr默认的最大值设定为50000。

（2）确定Nr后，对于一个给定的强度折减系数Fs，执行Nr步。在运行Nr步后，如果体系不平衡力比率R＜10－5，说明系统处于平衡状态。如果不平衡力比率R＞10－5那么继续执行Nr步，直到不平衡力比率R＜10－5。

在Flac3D中，边坡失稳的判据主要有三种：

（1）数值计算不收敛判据：采用强度折减法进行稳定性分析时，可通过判断计算是否收敛来作为边坡是否发生失稳的判据。数值方法通过强度折减使边坡达到极限破坏状态，滑动面上的位移和塑性变形将产生突变，且此位移和塑性应变的大小不再是一个定值，程序无法从数值方程组中找到一个既能满足静力平衡又能满足应力－应变关系和强度准则的解。此时，不管从力的收敛标准，还是从位移的收敛标准来判断数值计算都不收敛。此判据认为，在边坡破坏之前计算收敛，破坏之后计算不收敛，这表征滑动面上岩土体无限流动，因此可把静力平衡方程组是否有解，数值计算是否收敛作为边坡失稳破坏的判据。

（2）坡面位移突变判据：边坡的变形破坏总具有一定的位移特性，因此计算的位移结果是边坡失稳最直观的表达。目前以位移作为失稳判据的方法，是在计算过程中建立某个部位的位移或者最大位移与折减系数的关系曲线，以曲线上的拐点作为边坡处于临界破坏状态的临界点。也就是说，当折减系数增大到某一特定值时，某一部位的位移突然增大，则认为边坡发生失稳。

（3）塑性区贯通判据：由于岩土体是弹塑性的，当应力达到一定程度时，岩土体便会发生塑性破坏，岩土体的塑性破坏与塑性区出现扩展及其分布紧密相关。边坡破坏时，其塑性应变区域必然是贯通的。因此通过强度折减法进行边坡稳定性分析时，随着折减系数的不断增大，边坡各个部位必然会逐步发生不同程度的塑性变形。所以，如果发生塑性变形的区域相互贯通，那么说明边坡已经发生整体失稳。

研究表明：弹性模量对边坡安全系数几乎没有影响，但对边坡的位移分布和塑性区大小有直接影响；内聚力与安全系数几乎呈线性关系，并且随着内聚力的增加，滑动面由浅层向深层发展；内摩擦角与安全系数也几乎呈线性关系，但随着内摩擦角的增加，滑动面由深层向浅层发展［1］。