通过前面的例子可以看出，二次型的标准形不是唯一的.但是，所有的标准形具有一些共同的特征.

定理1（惯性定理）设二次型f=xTAx的秩为r，若有两个可逆变换

x=Py 及 x=Qz

使

及

则s=t=r，且k1,k2，…，ks与λ1，λ2，…，λt中正数的个数相等.

本定理不予证明.

简而言之，惯性定理断言所有的标准形含有相同的项数，且其中正系数的个数是相等的，这个数称为正惯性指数，而负系数的个数称为负惯性指数.

定义 1 若对任意x≠0，二次型f=xTAx＞0，则称f为正定二次型，A为正定矩阵；若对任意x≠0，二次型f=xTAx＜0，则称f为负定二次型，A为负定矩阵.

显然，n元二次型f=xTAx正定的充要条件为正惯性指数等于n，负定的充要条件为负惯性指数等于n.

下面给出一个从矩阵的角度出发判断正定或者负定的定理.

定理2 对称矩阵A正定的充要条件是它的各阶主子式都为正，即

对称阵A负定的充要条件是它的奇数阶主子式都为负，偶数阶主子式都为正，即

本定理不予证明.

例1　判断对称阵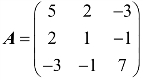的正定性.

解：计算各阶主子式(www.daowen.com)

由定理2知A是正定的.

例2　判断二次型f=−5x2−6y2−4z2+4xy+4xz的正定性.

解：f的矩阵为

计算各阶主子式

由定理2知f为负定二次型.

练习题（三）

1.判断二次型的正定性.

（1）；

（2）；

（3）.

2.t满足什么条件时，下列二次型是正定的.

（1）；

（2）.

3.证明：n元二次型f=xTAx正定的充要条件为正惯性指数等于n，负定的充要条件为负惯性指数等于n.