定义1 n元二次齐次多项式
称为二次型.
若取aji=aij,则2aijxixj=aijxixj+ajixjxi,于是式(1)可写为
再令A=(aij),xT=(x1,x2,…,xn),则式(2)化为
f(x1,x2,…,xn)=xTAx (3)
这便是二次型的矩阵表示.
注意,式(3)中A是一个对称阵,称为二次型f的矩阵,A的秩称为二次型f的秩.
特别地,如果二次型只含有平方项,即![]()
![]() ,则称其为二次型的标准形;如果在标准形中k1,k2,…,kn只在1,−1,0中取值,则称其为二次型的规范形.如果aij均为复数,则对应的二次型称为复二次型;如果aij均为实数,则对应的二次型称为实二次型.本书只讨论实二次型.
,则称其为二次型的标准形;如果在标准形中k1,k2,…,kn只在1,−1,0中取值,则称其为二次型的规范形.如果aij均为复数,则对应的二次型称为复二次型;如果aij均为实数,则对应的二次型称为实二次型.本书只讨论实二次型.
例1 求二次型![]() 的矩阵.
的矩阵.
解:由二次型矩阵的定义,有故所求矩阵为
a11=2,a22=0,a33=−1,a12=a21=−1,a13=a31=2,a23=a32=−1,
显然,二次型的标准形和规范形形式更为简洁,研究起来也比较方便.因此,我们想知道,二次型能否通过可逆变换化为标准形和规范形?为了回答这个问题,需要一些新的概念.
定义 2 设A与B是同阶方阵,若存在可逆矩阵C,使得B=CTAC,则称A与B合同.
合同关系具有以下性质:
(1)自反性:任何矩阵都与自身合同,即A与A合同.
(2)对称性:若A与B合同,则B与A也合同.
(3)传递性:若A与B合同,B与C合同,则A与C也合同.
容易看出,与对称阵合同的矩阵仍然是对称阵,且合同矩阵具有相同的秩.此外,对于实对称矩阵,相似一定合同,但合同不一定相似.而对于一般矩阵,相似不一定合同.例如,由于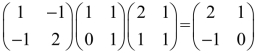 ,其中
,其中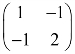 与
与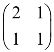 互为逆矩阵,故
互为逆矩阵,故 与
与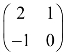 相似.但它们不合同,因此这是一个矩阵相似但不合同的例子.
相似.但它们不合同,因此这是一个矩阵相似但不合同的例子.
现在考虑化二次型为标准形的问题.若二次型f=xTAx经可逆变换x=Cy化为
则CTAC是对角阵.因此,上述过程可简述为寻找可逆矩阵C,使得CTAC成为对角阵.这个过程称为矩阵A的合同对角化.
我们知道,对于对称阵A,总有正交阵P,使得P−1AP=PTAP成为对角阵.将此结论应用到二次型,即有如下定理.(https://www.daowen.com)
定理1 对二次型f=xTAx,存在正交变换x=Py,使f=xTAx化为标准形
其中λ1,λ2,…,λn是A的n个特征值.
例2 用正交变换将二次型f=−2x1x2+2x1x3+2x2x3化为标准形.
解:二次型f的矩阵为
按照对称阵的对角化方法,求出
于是,有正交变换
将二次型f化为标准形
如果要继续化为规范形,可再做变换
即得规范形
练习题(一)
1.化下列二次型为矩阵表示.
(1)f=x2+4y2+z2+4xy+2xz+4yz;
(2)f=x2+y2−7z2−2xy−4xz−4yz;
(3)f=x2+y2+z2−2xy+6yz.
2.用正交变换化二次型为标准形,并求对应的变换矩阵.
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
3.证明: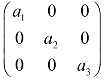 与
与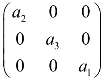 合同.
合同.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







