定义1　设有 2 个n维向量

令

(α，β)=a1b1+a2b2+…+anbn，

则称(α，β)为向量α与β的内积.

内积是两个向量之间的一种运算，其结果是一个实数，如果用矩阵记号表示，向量的内积还可写成

若向量α，β与γ为n维向量，λ为实数，则内积还满足下面运算规律：

（1）(α，β)=(β，α)；

（2）(λα，β)=λ(α，β)；

（3）(α+β，γ)=(α，γ)+(β，γ).

定义2　设

称||α||为n维向量α的长度或范数.

当||α||=1时，称α为单位向量.

对于任何非零向量α，α称为向量α的单位化.

向量的长度具有下述性质.

性质1　向量α与β为n维向量，λ为实数，则

（1）非负性：当α≠0时，||α||＞0，当α=0时，||α||=0；

（2）齐次性：||λα||=|λ|||α||；

（3）三角不等式：||α+β||≤||α||+||β||.(www.daowen.com)

定义3　向量α与β为n维非零向量，将

称为n维向量α与β的夹角.

定义4　当(α，β)=0时，称向量α与β正交，记为α ⊥β.

例1　判断向量与向量是否正交.

解：因为(α，β)=−2 ×4+1×(−7)+0 ×9+3 ×5=0，所以α ⊥β.

定义5　若非零向量组α1，α2，…，αm中任意2个向量都是正交的，则称这个向量组为正交向量组.

例2　对于n维单位向量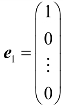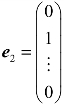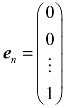，，…，，判断它们是否是正交向量组.

解：当i ≠j 时，(ei,ej)=0,i,j=1,2，…，n ；

当i=j 时，(ei,ej)=1,i,j=1,2，…，n .

所以单位向量组e1,e2，…，en是正交向量组.

定理1　若n维非零向量α1，α2，…，αm是正交向量组，则α1，α2，…，αm线性无关.

证明：用反证法.假设α1，α2，…，αm线性相关，则有m个不全为零的数s1,s2，…，sm，使得

s1α1+s2α2+…+smαm=0

以αiT左乘上式两端，得

αiT(s1α1+s2α2+…+smαm)=siαiTαi=0,i=1,2，…，m.

因αi≠0，故，从而si=0，(i=1,2，…，m)，与假设矛盾，于是向量组α1，α2，…，αm线性无关.