定义2　若n阶矩阵A与对角矩阵相似，则称A可对角化.

相似矩阵有许多共同性质.在我们熟悉的矩阵中，形式最简单的一类是对角矩阵，若矩阵A相似于对角矩阵，就可以借助对角矩阵来研究A.如何求相应的可逆矩阵P？下面就来讨论这个问题.

定理3　n 阶矩阵A相似于对角矩阵（A可对角化）的充要条件是A有 n个线性无关的特征向量.

证明：必要性.设存在可逆矩阵P，使得

设P=(α1，α2，…，αn)，由P−1AP=Λ，得AP=PΛ，

即

即

A(α1，α2，…，αn)=(λ1α1，λ2α2，…，λnαn)，

因此，Aαi=λαi(i=1,2，…，n).由于P可逆，因此|P|≠0，从而αi(i=1,2，…，n)都是非零向量，故α1，α2，…，αn分别是A的属于特征值λ1，λ2，…，λn的特征向量.再由P可逆知，α1，α2，…，αn线性无关.

充分性.设α1，α2，…，αn分别是A的属于特征值λ1，λ2，…，λn的n个线性无关的特征向量，则有

Aαi=λαi(i=1,2，…，n).

取P=(α1，α2，…，αn)，因为α1，α2，…，αn线性无关，所以P可逆，于是有

即

因此矩阵A相似于对角矩阵Λ.

因为特征向量不是唯一的，所以矩阵P不具有唯一性.

推论2　若n阶矩阵A有n个互异的特征值，则A必可对角化.

推论3　n阶矩阵A对角化的充分必要条件是A的每个ti重特征值λi都有ti个线性无关的特征向量.即r(λiE−A)=n−ti.

根据上述结论，可以归纳出将矩阵A对角化的具体计算步骤：

（1）求出n阶矩阵A的全部互异特征值λ1，λ2，…，λm，它们的重数依次为t1,t2，…，tm(t1+t2+…+tm=n).

（2）求A的特征向量.对每个特征值λi求方程组(λiE−A)x=0的基础解系，即为A的对应的线性无关的特征向量，设为

ξi1，ξi2，…，ξisi(i=1,2，…，m).

（3）判定A是否可对角化.若对每一个特征值都有si=ti(i=1,2，…，m)，则A可对角化，否则不可对角化.

（4）当A可对角化时，令

P=(ξ11，ξ12，…，ξ1s1，ξ21，ξ22，…，ξ2s2，…，ξm1，ξm2，…，ξmsm)

且P可逆，故有P−1AP=Λ.

例3　判断下列矩阵能否对角化，若可以对角化，求出可逆矩阵P，使P−1AP为对角矩阵.

解：（1）矩阵A的特征多项式为

由|λE−A|=0，得A的特征值为λ1=−1，λ2=1，λ3=3.由推论2 知，矩阵A可对角化.下面求可逆矩阵P.

对于λ1=−1，解齐次线性方程组(−E−A)x=0，即解方程组

得基础解系ξ1=(1，−1,0)T，ξ1即为A的属于特征值λ1=−1的一个特征向量.

对于λ2=1，解齐次线性方程组(E−A)x=0，即解方程组

得基础解系ξ2=(1，−1,1)T，ξ2即为A的属于特征值λ2=1的一个特征向量.

对于λ3=3，解齐次线性方程组(3E−A)x=0，即解方程组

得基础解系ξ3=(0,1，−1)T，ξ3即为A的属于特征值λ3=3的一个特征向量.

取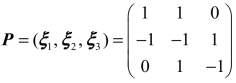，则有

（2）矩阵B的特征多项式为

由|λE−B|=0，得B的特征值为λ1=λ2=−1，λ3=5.其中，−1 为B的二重特征值.

对于λ1=λ2=−1，解齐次线性方程组(−E−B)x=0，即解方程组

由于

故r(−E−B)=3−2=1，依据推论3 知，矩阵B可对角化，且λ1=λ2=−1对应的线性无关的特征向量为ξ1=(−1,1,0)T，ξ2=(−1,0,1)T.

对于λ3=5，解齐次线性方程组(5E−B)x=0，即解方程组

得基础解系ξ3=(1 1,1)T，ξ3即为B的属于特征值λ3=3的一个特征向量.

取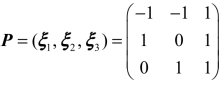，则有

对于可对角化的矩阵A，可以用P−1AP=Λ来求方阵的幂.

例4　设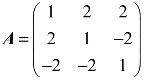，求Am（m为正整数）.

解：由例题3可知，取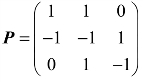，则有

则(www.daowen.com)

例5　设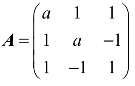，求a为何值时，

（1）A可对角化，并求相似变换矩阵P；

（2）A−E为可逆矩阵.

解：（1）矩阵A的特征多项式为

故A的特征值为λ1=λ2=a+1，λ3=a−2.

对于λ1=λ2=a+1，解齐次线性方程组((a+1)E−A)x=0，得A的属于特征值λ1=λ2=a+1的特征向量为ξ1=(1,1,0)T，ξ2=(1,0,1)T.

对于λ3=a−2，解齐次线性方程组((a−2)E−A)x=0，得A的属于特征值λ3=a−2的特征向量为ξ3=(−1,1,1)T.

依据推论3知，不论a为何值，矩阵A均可对角化.

令

则有

（2）因为A的特征值为a+1,a+1,a−2，从而A−E的特征值为a,a,a−3，故当a≠0且a≠3时，A−E为可逆矩阵.

练习题（二）

一、填空题

1.若A为四阶实对称矩阵，|A|=−8，且2是A的三重特征值，则A的相似对角矩阵为__________.

2.设A～B，其中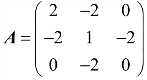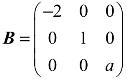，，则a=__________.

3.设A为n阶矩阵，A有n个互异特征值λ1，λ2，…，λn，则有r(λjE−A)=__________(j=1,2，…，n).

4.设A是三阶实对称矩阵，A的特征值是λ1=λ2=1，λ3=−1，则有A2n=__________.

5.若四阶矩阵A与B相似，矩阵A的特征值为，，，，则|B−1−E|=__________.

二、单选题

1.若可对角化的n阶矩阵A只有一个特征值为零，则r(A)=（　）.

A.n　B.n−1

C.1　D.0

2.当满足下列（　）条件时，矩阵A与B相似.

A.|A |=|B|

B.r(A)=r(B)

C.A与B有相同的特征多项式

D.n阶矩阵A与B有相同的特征值且n个特征值不相同

3.已知二阶实对称矩阵A的特征向量为，且|A|≤0，则必为A的特征向量的是（　）.

A.，c≠0

B.，c≠0

C.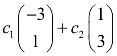，c1≠0,c2≠0

D.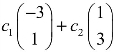，c1,c2不同时为零

4.设A是n阶非零矩阵，Ak=0，下列命题不正确的是（　）.

A.A的特征值只有零

B.A必不能对角化

C.E+A+A2+…+Ak−1必可逆

D.A只有一个线性无关的特征向量

5.设λ1，λ2是矩阵A的两个不同的特征值，对应的特征向量分别为α1，α2，则α1,A(α1+α2)线性无关的充要条件是（　）.

A.λ1=0

B.λ2=0

C.λ1≠0

D.λ2≠0

三、计算题

1.判断下列矩阵A与B是否相似.

2.求下列矩阵的k次幂.