定义1 设A,B为n阶矩阵,如果存在n阶可逆矩阵P,使得
P−1AP=B,
则称矩阵A和B相似,也称B是A的相似矩阵,记作A~B.可逆矩阵P称为相似变换矩阵.
例1 设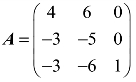 ,
,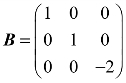 ,
,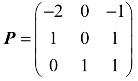 ,不难验证P可逆,且
,不难验证P可逆,且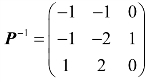 .
.
由于
因此A~B.
例2 设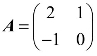 ,
,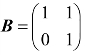 ,问A是否相似于B?
,问A是否相似于B?
解:因为存在可逆矩阵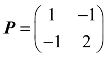 ,使得
,使得
所以,A相似于B.
相似是方阵之间的一种关系,这种关系具有如下性质.
性质1 (1)自反性:A~A;
(2)对称性:若A~B,则B~A;
(3)传递性:若A~B,B~C,则A~C.
此外,相似矩阵之间有许多共同的性质.
定理1 若n阶矩阵A与B相似,则:
(1)|A |=|B|;
(2)r(A)=r(B);
(3)A,B有相同的特征值;
(4)tr(A)=tr(B).
证明:由于A~B,故存在n阶可逆矩阵P,使得P−1AP=B,从而
(1)|B |=|P−1AP |=|P−1||A ||P |=|A|;
(2)r(B)=r(P−1AP)=r(AP)=r(A);
(3)由于|λE−B|=|λE−P−1AP |=|P−1(λE−A)P|=|λE−A|,即A,B有相同的特征多项式,于是A,B有相同的特征值;
(4)由(3)即得.
定理2 若n阶矩阵A与B相似,则
tr(AB)=tr(BA).
证明:设A=(aij),B=(bij),则AB的第i行第i列的元素为
所以
又由BA的第k行第k列的元素为
于是有
tr(AB)=tr(BA).
推论1 若n阶矩阵A与对角矩阵
相似,则λ1,λ2,…,λn是A的n个特征值.
证明:因λ1,λ2,…,λn是Λ的n个特征值,由定理1可知λ1,λ2,…,λn也就是A的n个特征值.
例2 若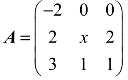 ,
, ,且A~B,求 x,y.(https://www.daowen.com)
,且A~B,求 x,y.(https://www.daowen.com)
解:对角矩阵B的特征值为−1,2,y,由于A~B,因此A的特征值也为 −1,2,y.再根据相似矩阵有相同的迹,可得
解此方程组得x=0,y=−2.
两个相似的矩阵还具有下面的性质.
性质2 (1)若A~B,则kA~kB;
(2)若A~B,且A,B均可逆,则A−1~B−1;
(3)若A~B,则Am~Bm(m为正整数);
(4)若A~B,且A,B均可逆,则A~B;
(5)若A~B,则AT~BT;
(6)若A~B,f(x)为x的多项式,则f(A)~f(B).
证明:(1)若A~B,则存在 n 阶可逆矩阵P,使得P−1AP=B,从而
P−1(kA)P=k(P−1AP)=k B,
从而kA~kB.
(2)若A~B,则存在n阶可逆矩阵P,使得P−1AP=B,从而
(P−1AP)−1=B−1,
即
P−1A−1P=B−1.
由于P可逆,P−1亦可逆,从而A−1~B−1.
(3)若A~B,则存在n阶可逆矩阵P,使得P−1AP=B,从而
从而Am~Bm.
(4)若A~B,则存在n阶可逆矩阵P,使得P−1AP=B.
又A,B均可逆,从而|A|≠0,|B|≠0.
由于
从而
A~B
(5)若A~B,则存在n阶可逆矩阵P,使得P−1AP=B,从而
BT=(P−1AP)T=PTAT(PT)−1,
由于方阵P可逆,则PT也可逆.从而AT~BT.
(6)设f(x)=a0xn+a1xn−1+a2xn−2+…+an−1x+an,则
f(A)=a0An+a1An−1+a2An−2+…+an−1A+anE,
f(B)=a0Bn+a1Bn−1+a2Bn−2+…+an−1B+anE.
若A~B,则存在n阶可逆矩阵P,使得P−1AP=B.由性质2(3)得
P−1AlP=Bl,l=1,2,…,n
从而
即f(A)~f(B).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







