从上面几个例题可以看出，在求矩阵的特征值和特征向量时，特征多项式的计算是很重要的.下面来考察其特征多项式某些系数的特征，并进而考察矩阵A与特征值λ1，λ2，…，λn的关系.

设A=(aij)n×n，则

利用行列式的定义计算行列式，知道其展开式中必有一项为主对角线上元素的乘积

(λ−a11)(λ−a22)…(λ−ann).

而展开式中的其余各项至多包含n−2 个主对角线上的元素，它对于λ的次数最多是n−2，因此特征多项式中含λ的n次与n−1 次的项只能在主对角线上元素的乘积中出现.

(λ−a11)(λ−a22)…(λ−ann)=λn−(a11+a22+…+ann)λn−1.

若在特征多项式中令λ=0，则得特征多项式的常数项为|−A|=(−1)n|A|.因此如果只列出特征多项式的前两项与常数项，则有

|λE−A|=λn−(a11+a22+…+ann)λn−1+…+(−1)n|A|.

由根与系数的关系知，A的全体特征值的和为a11+a22+…+ann，A的全体特征值的积为|A|.若将a11+a22+…+ann称为A的迹，记作tr(A)，则有下列性质成立.

性质1 n阶方阵A=(aij)n×n的所有特征根为λ1，λ2，…，λn（包括重根），则

（1）tr(A)=λ1+λ2+…+λn；

（2）|A |=λ1λ2…λn.

推论1　A可逆的充分必要条件是A的所有特征值都不为零.即

λ1λ2…λn=|A |≠0.

对应于矩阵A的特征值的特征向量，也有一些重要的结论.

定理2 n阶矩阵A与它的转置矩阵AT有相同的特征值.

证明：|λE−AT|=|(λE−A)T|=|λE−A|.

定理3　设λ是A的特征值，且α是A属于λ的特征向量，则：

（1）kλ是kA的特征值，并有(kA)α＝(kλ)α；

（2）λk是Ak的特征值，Akα＝λkα；

（3）若A可逆，且λ≠0，则是A−1的特征值，即A−1；

（4）若φ(x)为x的多项式，则φ(x)为φ(A)的特征值.

证明：因为α是A属于λ的特征向量，有Aα=λα.

（1）两边同时左乘k得：(kA)α=(kλ)α，则kλ是kA的特征值.

（2）Akα＝Ak−1(Aα)=Ak−1(λα)=λAk−2(Aα)=λAk−2(λα)=λ2(Ak−2α)

=…=λk−1(Aα)=λkα，

则λk是Ak的特征值.

（3）因为A可逆，所以它所有的特征值都不为零.

由Aα＝λα，得A−1(Aα)=A−1(λα)，即

(A−1A)α=λ(A−1α)⇒α=λ(A−1α).

再由λ≠0，两边同除以λ得：

所以λ≠0时是A−1的特征值.

（4）设φ(x)=a0xm+a1xm−1+…+am−1x+am，则

φ(A)α=(a0Am+a1Am−1+…+am−1A+amE)α

=a0Amα+a1Am−1α+…+am−1Aα+amEα

=a0λmα+a1λm−1α+…+am−1λα+amα

=(a0λm+a1λm−1+…+am−1λ+am)α

=φ(λ)α.

定理4　设λ1，λ2，…，λr是A的r个互不相同的特征值，α1，α2，…，αr分别是与λ1，λ2，…，λr对应的特征向量，则α1，α2，…，αr线性无关.即不同特征值的特征向量线性无关.

证明：设有常数k1,k2，…，kr，使得

k1α1+k2α2+…+krαr=0，　（8）

上式两边左乘A，并注意到Aαi=λiαi(i=1,2，…，r)，有

k1λ1α1+k2λ2α2+…+krλrαr=0，

按这种方法再依次用A2,A3，…，Ar−1左乘式（8），并应用定理3（4）的结论，得

上式的矩阵形式为

上式左端第二个矩阵的行列式是范德蒙行列式，因为λ1，λ2，…，λr互不相同，所以该行列式的值不为零，从而该矩阵可逆.用该矩阵的逆右乘上述等式两边，得

(k1α1,k2α2，…，krαr)=(0,0，…，0)

于是

kiαi=0,i=1,2，…，r，

由于特征向量αi,i=1,2，…，r 非零，因此只有ki=0,i=1,2，…，r 上式才能成立，故α1，α2，…，αr线性无关.

推论2　设λ1，λ2，…，λr是A的r个互不相同的特征值，a11,a12，…，a1k1是对应于λ1的k1个线性无关的特征向量，……，ar1,ar2，…，arkr是对应于λr的kr个线性无关的特征向量，则向量组a11,a12，…，a1k1，……，ar1,ar2，…，arkr也是线性无关的.即对于互不相同的特征值，取它们各自的线性无关的特征向量，把这些特征向量放在一起合成的向量组仍是线性无关的.

例5　已知三阶方阵A，有一特征值是 3，且tr(A)=|A|=6，求A的所有特征值.

解　设A的特征值为 3，λ2，λ3，由上述性质得：

λ2+λ3+3=tr(A)＝6，

λ2·λ3·3=|A|＝6，

由此得：λ2=1，λ3=2.

例6　已知三阶方阵A的三个特征值是 1，−2，3，求：(www.daowen.com)

（1）|A|；（2）A−1的特征值；（3）AT的特征值；（4）A*的特征值.

解：（1）|A|＝1×(−2)×3＝−6；

（2）A−1的特征值为：1，，；

（3）AT的特征值为：1，−2，3；

（4）A*＝|A|A−1＝−6A−1，则A*的特征值为：−6×1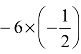，，，即为：−6，3，−2.

例7　已知矩阵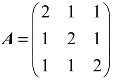，且向量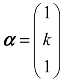是逆矩阵A−1的特征向量，试求常数k.

解：设λ是A对于α的特征值，所以Aα=λα，即

得

从而

例8　设A为n阶方阵，证明|A|=0的充要条件是 0 为矩阵A的一个特征值.

证明：为矩阵A的一个特征值.

例9　若A2=0，则A的特征值只能是零.

证明：设λ是矩阵A的任一特征值，α是对应的特征向量，则

Aα=λα

所以0=A2α=A( Aα)=λ2α，而α≠0，所以λ=0.

例10　设n阶方阵A满足A2−5A+6E=0.证明：A的特征值只能是2和3.

证明：设λ是A对于特征向量α的特征值，则Aα=λα.因此

因α≠0，所以

λ2−5λ+6=0，

即

λ=2或λ=3.

例11　设4阶矩阵满足|3E+A|=0，AAT=4E，|A|＜0，求A*的一个特征值.

解：由|3E+A|=0知，

|3E+A |=|A−(−3E)|=0，

即λ=−3是A的一个特征值.现设α是与之对应的特征向量，则Αα=−3α.

又|A|2=|AAT|=|4E|=44，且|A|＜0，所以|A|=−16.

在Αα=−3α两端同时左乘A*得：

−3A*α=A*Aα=−16α，

即

故A*的一个特征值为.

练习题（一）

一、填空题

1.矩阵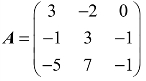的特征值__________.

2.A为n阶矩阵，Ax=0有非零解，则A必有一个特征值__________.

3.若n阶可逆方阵A的每行元素之和为a，则3A−1+E的一个特征值为__________.

4.设A为三阶可逆矩阵，其逆矩阵的特征值为，，，则行列式|E−A|=__________.

5.设λ=2是非奇异矩阵的一个特征值，则矩阵有一个特征值为__________.

二、单选题

1.设三阶矩阵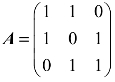，则A的特征值是（　）.

A.1，0，1　B.1，1，2

C.−1，1，2　D.1，−1，1

2.若A2=A，且A ≠E，则以下结论错误的是（　）.

A.|A−E|≠0

B.(A+E)−1=−(A−2E)

C.A为不可逆矩阵

D.A必有特征值λ≠0

3.设，A有特征值λ1=6，λ2=2（二重），且A有三个线性无关的特征向量，则x=（　）.

A.4

B.2

C.−4

D.−2

三、计算题

1.求矩阵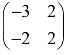的特征值与特征向量.

2.求矩阵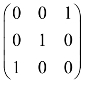的特征值与特征向量.

3.求矩阵的特征值与特征向量.

4.求矩阵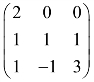的特征值与特征向量.