下面先列举一个例子，然后介绍矩阵A的特征值与特征向量的求法.

例1　求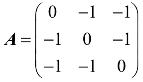的特征值和特征向量.

解：先写出A的特征多项式

再求特征多项式的根，即解方程

(λ+2)(λ−1)2=0，

得到A的3个特征值为λ1=−2，λ2=λ3=1.

注　求矩阵 A 对应于特征值λ0的特征向量.利用式（2），将λ=λ0代入式 （2），求出该齐次线性方程组的所有非零解，这些解均为对应于λ0的特征向量.

当λ1=−2时，解齐次线性方程组

(−2E−A)X=0，　（6）

把系数矩阵通过初等行变换化为阶梯形矩阵，即

可知r(−2E−A)=2，取x3为自由未知量，得到方程组（6）的基础解系为α1=(1,1,1)T，于是A的属于特征值−2 的全部特征向量为k1α1，其中k1是不为零的常数.

当λ2=λ3=1时，解齐次线性方程组

(E−A)X=0，　（7）

为此先对矩阵E−A做初等行变换化为阶梯形矩阵：

可知r(E−A)=1，取x2,x3为自由未知量，得到方程组（7）的基础解系为α2=(−1,1,0)T，α3=(−1,0,1)T，所以A的属于特征值 1 的全部特征向量为k2α2+k3α3，其中k2,k3为不全为零的常数.

由此可以得到两个重要结论：

（1）矩阵A对应于特征值λ0的特征向量乘以非零常数k仍为对应于λ0的特征向量；

（2）矩阵A对应于同一个特征值λ0的2个特征向量之和仍为对应于λ0的特征向量.

上述关于矩阵A的特征值及特征向量的求法的结论，可归纳为如下定理.

定理1　设A是n阶矩阵，λ是A的特征值，则α是A的属于λ的特征向量的充分必要条件是λ是|λE−A|＝0的根，α是齐次线性方程组(λE−A)X=0的非零解.

由定理1可归纳出求矩阵A的特征值及特征向量的步骤：

（1）计算|λE−A|；

（2）求|λE−A|＝0 的全部根，它们就是A的全部特征值λ1，λ2，…，λn；

（3）对于矩阵A的每一个特征值λi，求出齐次线性方程组(λiE−A)X=0的一个基础解系：η1，η2，…，ηn−r，其中r为矩阵λiE−A的秩；

则矩阵A的属于λi的全部特征向量为：

k1η1+k2η2+…+kn−rηn−r，(www.daowen.com)

其中k1,k2，…，kn−r为不全为零的常数.

例2 求的特征值和特征向量.

解：先写出A的特征多项式，

再求特征多项式的根，即解方程

(λ−1)(λ−3)2=0，

得到A的3个特征值为λ1=1，λ2=λ3=3.

当λ1=1时，解齐次线性方程组

(E−A)X=0，

把系数矩阵通过初等行变换化为阶梯形矩阵，即可知r(E−A)=2，取x3为自由未知量，得到方程组(E−A)X=0的基础解系为α1=(−1，−1,1)T，于是A的属于特征值 1 的全部特征向量为k1α1，其中k1是不为零的常数.

当λ2=λ3=3时，解齐次线性方程组

(3E−A)X=0，

为此先对矩阵(3E−A)做初等行变换化为阶梯形矩阵，

可知r(3E−A)=2，取x3为自由未知量，得到方程组(3E−A)X=0的基础解系为α2=(−1，−3,1)T，于是A的属于特征值 3 的全部特征向量为k2α2，其中k2是不为零的常数.

例3　求的特征值及对应的特征向量.

解：

令|λE−A|＝0 解得：λ1=−1，λ2=1，λ3=3.

当λ1=−1时，；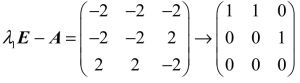

r(λ1E−A)=2，取x2为自由未知量，对应的方程组为，解得一个 基础解系为α1=(−1,1,0)T，所以A的属于特征值　−1的全部特征向量为k1α1，其中k1是不为零的常数.

当λ2=1时，，r(λ2E−A)=2，取x3为自由未知量，对应的方程组为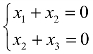，解得一个基础解系为α2=(−1,1，−1)T，所以A的属于特征值 3 的全部特征向量为k2α2，其中k2是不为零的常数.

当λ3=3时，，r(λ3E−A)=2，取x3为自由未知量，对应的方程组为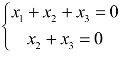，解得一个基础解系为α3=(0，−1,1)T，所以A的属于特征值3的全部特征向量为k3α3，其中k3是不为零的常数.

例4　已知矩阵有一个特征向量，求x的值.

解：由已知有

得

所以有