设有非齐次线性方程组：

它也可写作向量方程

AX=b　（5）

非齐次线性解向量具有以下性质：

性质3　设η1，η2是非齐次线性方程组（5）的解，则η1−η2是其导出组AX=0的解.

性质4　设η0是非齐次线性方程组（5）的一个特解，ξ为其导出组AX=0的通解，则ξ+η0为非齐次线性方程组（5）的通解.

根据性质4，在求解非齐次线性方程组时，可以先求出一个特解η0和其导出组的通解ξ，再通过ξ+η0就可以得到非齐次线性方程组的通解.

例2　求非齐次线性方程组的解.

解：对增广矩阵施行初等行变换变为行阶梯形矩阵，

因为r(B)=r(A)=2 ＜4，所以非齐次线性方程组有无穷多解.

取自由未知数为x2,x3，原方程组与方程组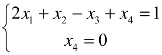同解，

取x2=x3=0，代入上式得非齐次线性方程组的一个特解为：.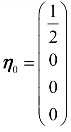

再求其导出组的基础解系，其导出组与方程组同解，

对自由未知数分别取为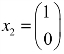，，代入上式得到其导出组的一个基础解系为：，.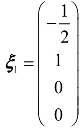

则原方程组的全部解为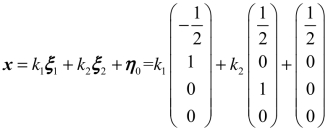：（k1,k2为任意常数）.

例3　求解非齐次线性方程组.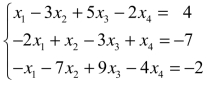

解：对增广矩阵施行初等行变换变为行阶梯形矩阵，

可得，其中x3,x4为自由未知数.

取x3=x4=0，得非齐次线性方程组的一个特解为：.

在对应的齐次线性方程组中，取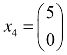，，代入上式得到其导出组的一个基础解系为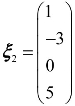：，.(www.daowen.com)

于是，所求通解为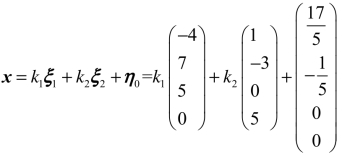（k1,k2为任意常数）.

例4　设四元非齐次线性方程组Ax=b的系数矩阵A的秩为3，已知它的三个解向量为η1，η2，η3，其中η1=(1,2,3,4)T，η2+η3=(0,1,2,3)T，求方程组的通解.

解：因为A的秩为3，则Ax=0的基础解系含有n−r=4−3=1个解向量.

由线性方程组解的性质得：η2+η3−2η1=(η2−η1)+(η3−η1)是Ax=0的解，

则解得Ax=0的一个非零解为：η2+η3−2η1=(−2，−3，−4，−5)T.

由此可得Ax=b的通解为：(1,2,3,4)T+k(2,3,4,5)T.

注：设有非齐次线性方程组Ax=b，而α1，α2，…，αn是系数矩阵A的列向量组，则下列四个命题等价：

（1）非齐次线性方程组Ax=b有解；

（2）向量b能由向量组α1，α2，…，αn线性表示；

（3）向量组α1，α2，…，αn与向量组α1，α2，…，αn,b等价；

（4）b属于A的列空间，即b∈C(A)；

（5）r(A)=r(A,b).

练习题（六）

1.求齐次线性方程组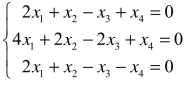的一个基础解系.

2.求齐次线性方程组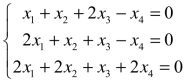的一个基础解系.

3.证明性质4：设η是非齐次线性方程组Ax=b的特解，ξ为其导出组AX=0的通解，则ξ+η为非齐次线性方程组AX=b的通解.

4.求解非齐次线性方程组.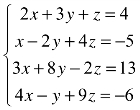

5.设四元非齐次线性方程组AX=b的系数矩阵A的秩为3，已知它的三个解向量为η1，η2，η3，其中η1=(3，−4,1,2)T，η2+η3=(4,6,8,0)T，求方程组的通解.