定义1　右端常数项全为零的线性方程组叫作齐次线性方程组；右端常数项不全为零的线性方程组叫作非齐次线性方程组.

当系数矩阵相同时，称齐次线性方程组为非齐次线性方程组的导出组.

设有齐次线性方程组：

若记，，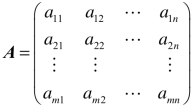

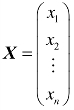则方程组（1）可写为向量方程

AX=0　（2）

称方程组（2）的解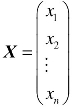为方程组（1）的解向量.显然，零向量一定是齐次线性方程组（1）的解向量；如果齐次线性方程组有非零解，则它必定有无穷多解.

根据向量方程组（2），可以讨论齐次线性解向量的性质：

性质1　若ξ1，ξ2为方程组（2）的解，则ξ1+ξ2也是该方程组的解.

性质2　若ξ1为方程组（2）的解，k为实数，则kξ1也是该方程组的解.

性质1，2说明，对于齐次线性方程组而言，解的线性组合仍然是方程组的解.根据向量空间的定义，线性方程组AX=0的全体解向量所构成的集合对于加法和数乘是封闭的，因此构成一个向量空间，称此向量空间为齐次线性方程组AX=0的解空间.若能求出解空间的基，那么就能用它的线性组合表示这个齐次线性方程组的全部解.

定义2　齐次线性方程组AX=0的有限个解ξ1，ξ2，…，ξt满足：

（1）ξ1，ξ2，…，ξt线性无关；

（2）AX=0的任意一个解均可由ξ1，ξ2，…，ξt线性表示； 则称ξ1，ξ2，…，ξt是齐次线性方程组AX=0的一个基础解系.

注：方程组AX=0的一个基础解系即为其解空间的一个基，易见方程组AX=0的基础解系不是唯一的，因此其解空间的表示形式也不唯一.(www.daowen.com)

按上述定义，若ξ1，ξ2，…，ξt是齐次线性方程组AX=0的一个基础解系，则AX=0的任一解可表示为X=k1ξ1+k2ξ2+…+ktξt，其中k1,k2，…，kt为任意常数.

当一个齐次线性方程组只有零解时，该方程组没有基础解系；而当一个齐次线性方程组有非零解时，是否一定有基础解系呢？如果有，如何求它的基础解系？下面的定理1回答了这两个问题.

定理1　对齐次线性方程组AX=0，若系数矩阵A的秩r ＜n，则该方程组的基础解系一定存在，且每个基础解系中所含解向量的个数均等于n−r，其中n是方程组所含未知量的个数.

若已知ξ1，ξ2，…，ξn−r是线性方程组AX=0的一个基础解系，则AX=0的全部解可表示为

x=k1ξ1+k2ξ2+…+kn−rξn−r　（3）

其中k1,k2，…，kn−r为任意实数.称表达式（3）是线性方程组AX=0的通解.

定理1可以通过矩阵初等行变换进行证明，这里略过，只通过例1展示如何求齐次线性方程组的基础解系.在选择n−r个自由未知数时，可以分别选为n−r个单位坐标向量ε.基础解系不唯一，因此得到的通解表达形式也不唯一.

当系数矩阵的秩r=n时，方程组AX=0只有零解，此时解空间V只含有一个零向量，解空间V的维数为0.当r ＜n时，方程组AX=0必含有n−r个向量的基础解系ξ1，ξ2，…，ξn−r，解空间V的维数为n−r；此时，方程组的任一解可表示为x=k1ξ1+k2ξ2+…+kn−rξn−r，其中k1,k2，…，kn−r为任意实数.解空间V可表示为V={x |x=k1η1+k2η2+…+kn−rηn−r,k1,k2，…，kn−r∈R}.

例1　求齐次线性方程组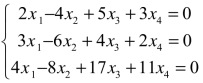的一个基础解系，并用此基础解系表示它的全部解.

解：

因为r(A)=2 ＜4，所以齐次线性方程组有无穷多解.取自由未知数为x2,x4，原方程组与方程组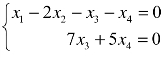同解；

对自由未知数分别取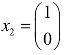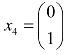，，代入上式得到齐次线性方程组的一个基础解系为：，.

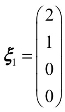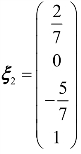则齐次线性方程组的全部解为：（k1,k2为任意常数）.