定义5 矩阵A的列（行）向量生成的子空间，称为矩阵的列（行）空间，记作C(A)（C(AT)）.

若A是m ×n实矩阵，A的列向量组α1，α2，…，αn∈Rm，行向量组β1，β2，…，βm∈Rn，则C(A)=L(α1，α2，…，αn)是Rm的一个子空间，C(AT)=L(β1，β2，…，βm)是Rn的一个子空间.

列空间是一个非常重要的概念，本章第二节讲过，方程组Ax=b有解等价于向量b能被向量组A：α1，α2，…，αn线性表示，即向量b是矩阵A的列向量组的线性组合.根据矩阵列空间的定义，这个充要条件也可以叙述为“b属于A的列空间，即b∈C(A)”.换句话说，如果向量b不属于A的列空间，则线性方程组Ax=b无解.

例5 设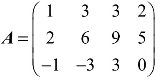，求A的列空间C(A)的基.

解：对矩阵A施行初等行变换变为行阶梯形矩阵：

矩阵U的第1，3列是U的列向量组的最大无关组，与之对应的A的第1，3列是A的列向量组的最大无关组，所以α1=(1,2，−1)T，α3=(3,9,3)T是C(A)的一组基.

练习题（五）(www.daowen.com)

1.用向量空间的定义证明：两个n维向量α和β的线性组合构成的集合是一个向量空间.

2.利用定义判断集合是否是向量空间.

3.判断向量组α1=(1,1,1)T，α2=(1,2,1)T，α3=(2,1，−1)T是否为R3的基；若是，则求出向量α=(1,5,7)T在该基下的坐标.

4.设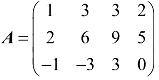，求A的行空间C(AT)的基.

5.已知矩阵A，向量b和b*均属于A的列空间，试证明b+b*也属于A的列空间.