定义1 设有两个n维向量组A ：α1，α2，…，αm和B ：β1，β2，…，βl，若向量组B中的每个向量都能被向量组A线性表示，则称向量组B能由向量组A线性表示.若向量组A与向量组B能互相线性表示，则称这两个向量组等价.

向量组A和B可以依次构成两个矩阵，分别记作A=(α1，α2，…，αm)和B=(β1，β2，…，βl).根据定义，向量组B能由向量组A线性表示，即对B中的每个向量βj(j=1,2，…，l)都存在m个常数k1j,k2j，…，kmj，使得

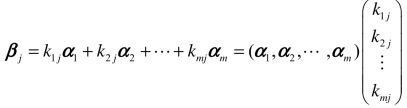，从而

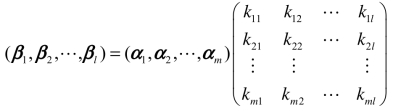，其中矩阵Km×l=(kij)称为这一线性表示的系数矩阵.

由此可知，若Bn×l=An×mKm×l，则矩阵B的列向量组能由矩阵A的列向量组线性表示，K为这一表示的系数矩阵.

类似地，可分析得矩阵B的行向量组能由矩阵K的行向量组线性表示，A为这一表示的系数矩阵.

定理1 向量组B ：β1，β2，…，βl能由向量组A ：α1，α2，…，αm线性表示的充要条件是矩阵A=(α1，α2，…，αm)的秩等于矩阵(A,B)=(α1，α2，…，αm，β1，β2，…，βl)的秩，即r(A)=r(A,B).

证明：向量组B ：β1，β2，…，βl能由向量组A ：α1，α2，…，αm线性表示，

例1 设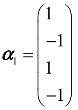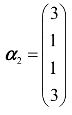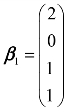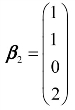，，，，，试证明向量组α1，α2与向量组β1，β2，β3等价.(www.daowen.com)

证明：记A=(α1，α2)，B=(β1，β2，β3)，则

显然，r(A)=2=r(A,B)，故向量组B能由向量组A线性表示；

因为r(B)≤2且B中有二阶非零子式；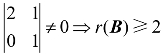

所以r(B)=2，即有r(B)=2=r(A,B)，故向量组A能由向量组B线性表示.

综上，向量组α1，α2与向量组β1，β2，β3等价.

向量组等价具有传递性，下面给出传递性的描述.

引理　若向量组A可由向量组B线性表示，向量组B可由向量组C线性表示，则向量组A可由向量组C线性表示.