若干个维数相同的列向量（或相同维数的行向量）所组成的集合叫作向量组.例如一个m ×n矩阵A的全体列向量就组成一个向量组，这个向量组中有n个m维的列向量，称为矩阵A的列向量组，记为A ：α1，α2，…，αn，其中.

定义 5 给定向量组A ：α1，α2，…，αn，对于任意一组实数k1,k2，…，kn，称关系式k1α1+k2α2+…+knαn为向量组A的一个线性组合，其中k1,k2，…，kn称为这个线性组合的系数.给定向量组A ：α1，α2，…，αn和向量β，如果存在一组实数λ1，λ2，…，λn，使得β=λ1α1+λ2α2+…+λnαn成立，则称向量β是向量组A的线性组合，也称向量β可由向量组A ：α1，α2，…，αn线性表示.显然，零向量是任何一组同维向量组的线性组合.

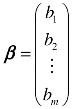实际上，线性方程组也可以简写成向量组的线性组合形式，例如线性方程组就可以表示为x1α1+x2α2+…+xnαn=β或(α1，α2，…，αn)x=β，其中，，.线性方程组有解等价于向量β可以被向量组A ：α1，α2，…，αn线性表示.

例2 设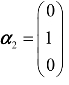，，，，判断β能否由向量组α1，α2，α3线性表示，并求出表示式.

解：设x1α1+x2α2+x3α3=β，即.

解出x1=1，x2=2，x3=3，故β可以由向量组α1，α2，α3线性表示，表示式为β=α1+2α2+3α3.

n维单位矩阵E的列向量叫作n维单位坐标向量，将例2的结论推广开来：任意n维列向量均可以表示为单位坐标向量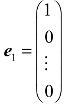，，…，的线性组合.

实际上，判定向量能否被向量组线性表示的问题，就是判定线性方程组x1α1+x2α2+…+xnαn=β是否有解，也可以转换为判断矩阵的秩的问题.

定理1 向量β能由向量组A ：α1，α2，…，αn线性表示的充分必要条件是矩阵A=(α1，α2，…，αn)的秩等于矩阵B=(α1，α2，…，αn，β)的秩.

例3 设，，，，证明β可以由向量组α1，α2，α3线性表示，并求出表示式.

证明：令A=(α1，α2，α3)，B=(α1，α2，α3，β)，

则.

显然r(A)=r(B)，所以β可以由向量组α1，α2，α3线性表示.(www.daowen.com)

由行最简形矩阵，可写出方程组的解.

故β=(α1，α2，α3)x=(2−3c1)α1+(1+2c1)α2+c1α3，其中c1为任意常数.

练习题（二）

1.已知向量α1=(1,1,0)T，α2=(0,1,1)T，α3=(3,4,0)T，求α1−α2，3α1+2α2−α3.

2.已知向量α=(3,2，−1,0)T，β=(−1,5,2,0)T，且满足2α+γ=β，求向量γ.

3.设3(α1−α)+2(α2+α)=5(α3+α)，其中α1=(2,5,1,3)T，α2=(10,1,5,10)T，α3=(4,1，−1，−1)T，求α.

4.已知，，，，，判断β能否由向量组α1，α2，α3，α4线性表出，并求出表示式.

5.已知向量α1=(1，λ，3)T，α2=(2,1,1)T，α3=(0,1,4)T，β=(1,2,1)T，求参数λ的取值范围，使向量β可由α1，α2，α3线性表示.

6.设α1=(1,1，λ)T，α2=(1，λ，1)T，α3=(λ，1,1)T，β=(λ2，λ，1)T，求解以下三个问题：

（1）λ为何值时，β能由α1，α2，α3唯一地线性表示？

（2）λ为何值时，β能由α1，α2，α3线性表示，但表达式不唯一？

（3）λ为何值时，β不能由α1，α2，α3线性表示？