二维、三维向量之间的最基本的运算是向量的加法和数量乘法,对于n维向量,也可做类似的操作.
定义 3 两个n维向量α=(a1,a2,…,an)与β=(b1,b2,…,bn)的对应分量之和构成的向量,称为向量α与β的和向量,记为α+β,即α+β=(a1+b1,a2+b2,…,an+bn).由向量的加法及负向量的定义,可以定义向量的减法:
α−β=α+(−β)=(a1−b1,a2−b2,…,an−bn).
定义 4 n维向量α=(a1,a2,…,an)的各分量都乘以数k所构成的向量,称为数k与向量α的数量乘积,记为kα,即kα=(ka1,ka2,…,kan).
显然,k·0=0,0·α=0;如果k≠0,α≠0,则kα≠0.
向量的加法与数量乘积统称为向量的线性运算.
例1 已知向量α1=(1,4,5),α2=(2,0,−3),α3=(−3,1,4),计算2α1−α2+α3.
解:2α1−α2+α3=2(1,4,5)−(2,0,−3)+(−3,1,4)
=(2,8,10)−(2,0,−3)+(−3,1,4)
=(−3,9,17).
向量的线性运算满足下列八条运算规律:
(1)α+β=β+α;(https://www.daowen.com)
(2)α+(β+γ)=(α+β)+γ;
(3)α+0=α;
(4)α+(−α)=0;
(5)(k+l)α=kα+lα ;
(6)k(α+β)=kα+kβ ;
(7)k(lα)=(kl)α;
(8)1·α=α.
其中α,β,γ是n维向量,k,l是实数.
以上运算规律根据向量加法和数乘的定义,可以简单证明,此处略过.
n维向量可以写为行的形式,如αΤ=(a1,a2,…,an),称为行向量;也可以写为列的形式,如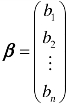 ,称为列向量.列向量之间加法、数量乘法的定义及性质与上面的讨论完全类似.行向量和列向量可以通过转置运算相互转换,如
,称为列向量.列向量之间加法、数量乘法的定义及性质与上面的讨论完全类似.行向量和列向量可以通过转置运算相互转换,如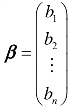 ,而βT=(b1,b2,…,bn).如未做特别说明,在本书中约定用α,β,γ,…表示列向量,用αT,βT,γT,…表示行向量.
,而βT=(b1,b2,…,bn).如未做特别说明,在本书中约定用α,β,γ,…表示列向量,用αT,βT,γT,…表示行向量.
行向量和列向量均可视为特殊的矩阵进行处理,因此行向量αΤ和列向量β也可以做矩阵乘法的运算,即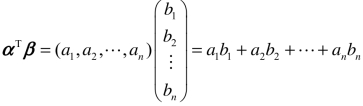 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





