上述消元法的过程，给出了n元线性方程组Ax=b的解的判定定理.

定理1 线性方程组解的判定定理.

对于n元线性方程组Ax=b：

（1）无解的充分必要条件是r(A)＜r(B)；

（2）有唯一解的充分必要条件是r(A)=r(B)=n ；

（3）有无穷多解的充要条件是r(A)=r(B)＜n .

定理1可以由线性方程组的消元法过程证明，这里简单给出证明的思路.实际上，消元法解方程的三个基本变换，对应着矩阵的三种初等变换.对方程组（1）做消元法变换等同于对线性方程组的增广矩阵做初等行变换，方程组（2）的增广矩阵则对应经初等行变换后所得到的行阶梯形矩阵.方程组（2）解的三种情况可以通过比较系数矩阵的秩与增广矩阵的秩得到：

①　dr+1≠0，即r(A)＜r(B)，此时线性方程组无解；

②　dr+1=0且r=n，即r(A)=r(B)=n，此时线性方程组有唯一解；

③　dr+1=0且r ＜n，即r(A)=r(B)＜n，此时线性方程组有无穷多解.

因此，判断线性方程组是否有解的问题，可以转换为判断线性方程组系数矩阵与增广矩阵的秩的大小问题.

例2 求解线性方程组.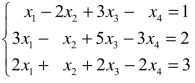

解：对增广矩阵B施行初等行变换变为行阶梯形矩阵，

可见r(A)=2，r(B)=3，r(A)＜r(B)，故方程组无解.

例3 求解线性方程组.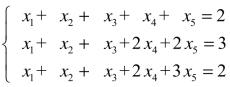

解：对增广矩阵B施行初等行变换变为行阶梯形矩阵，(www.daowen.com)

可见r(A)=r(B)=3 ＜5，故方程组有无穷多解.为简化回代过程中的计算，继续对行阶梯形矩阵实行初等变换，将其变为行最简形矩阵.

该矩阵对应的线性方程组为，

解得.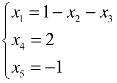

令x2=c1,x3=c2，则线性方程组的解为.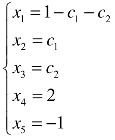

根据定理1，当r(A)=r(B)＜n 时，线性方程组有无穷多解.此时，B的行阶梯形矩阵中有r个非零行，取这r个非零行第一个非零元所对应的未知数作为非自由未知数，其余n−r个未知数作为自由未知数，令自由未知数等于c1,c2，…，cr，即可写出线性方程组的解.

例4 λ取何值时，线性方程组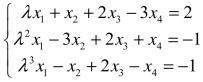有解？

解：对该方程组的增广矩阵做初等行变换，

据定理1，当r(A)=r(B)时，线性方程组有解.容易看出r(B)=3，要使r(A)=3，必须−2λ3+λ2+λ≠0.所以当λ≠0且λ≠1且时，原方程组有解.

练习题（一）

1.用消元法求解线性方程组.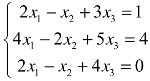

2.求解线性方程组.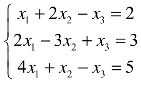

3.判断线性方程组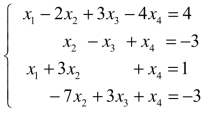是否有解；若有解，求出方程组的解.

4.求解线性方程组.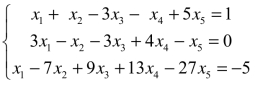

5.λ取何值时，线性方程组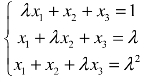有解？若有解，求出方程组的解.