所谓方程组（1）的一个解，指的是由n个数组成的有序数组(k1,k2，…，kn)，当分别用k1,k2，…，kn代入方程取代x1,x2，…，xn后，方程组（1）中每个等式变为恒等式，方程组（1）的解的全体称为它的解集合.解方程组实际上就是找出它的全部解，或者说，求出它的解集合.如果两个方程组有相同的解集合，它们就称为同解的.本章第六节还会专门对线性方程组解的结构进行讨论.

在中学代数里，已经学习过用加减消元法和代入消元法解二元、三元线性方程组.

例1 求解线性方程组.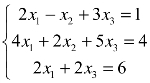

解：利用消元法解方程组

将x3=−6代入方程②和①，解得x2=−1，x1=9，即方程组的解为.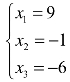

消元法实际上就是反复地对方程组进行变换，所做的变换由以下三种基本变换构成：

（1）互换两个方程的位置；

（2）方程两端同乘以k；

（3）把一个方程的k倍加到另一方程.(www.daowen.com)

可以证明，变换前后方程组的解不变，即变换前后的方程组是同解的.采用消元法求解一般线性方程组，一步一步变换下去，最终会得到一个形如式（2）的阶梯形方程组.显然，方程组（2）和方程组（1）是同解的.

根据dr+1的取值以及r与n的大小关系，可分以下几种情况讨论方程组（2）的解：

（1）如果dr+1≠0，就出现了零等于非零的矛盾情况，意味着无论x1,x2，…，xn取什么值，方程组都无解，即方程组（1）无解.

（2）如果dr+1=0，或者方程组（2）中没有0=0这种方程时，有两种可能：

①　r=n.

此时，阶梯形方程组为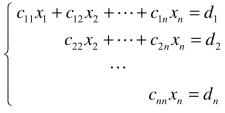，显然方程组有解，且有唯一解，可用回代法依次求出xn,xn−1，…，x1.

②　r ＜n.

此时阶梯形方程组为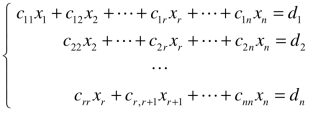，其中crr≠0.通过移项，将它改写为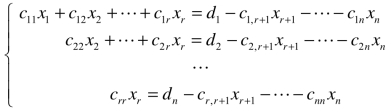.接下来，采用回代法，用xr+1，…，xn表示出x1,x2，…，xr.显然，方程组有解，且有无穷多解.