线性代数：分块矩阵的运算规则与普通矩阵类似

分块矩阵的运算规则与普通矩阵的运算规则类似.

1.分块矩阵的加法与数乘

设矩阵A,B是同型矩阵，采用相同的分块法，如

其中Aij与Bij(i=1,2，…，s； j=1,2，…，r)的行数相同、列数相同，则

分块矩阵的加法：

分块矩阵的数乘：

2.分块矩阵的转置

设，则.

3.分块矩阵的乘法

设A是m ×l矩阵，B是l ×n矩阵，分块成

其中Ai1,Ai2，…，Ait(i=1,2，…，s)的列数分别等于B1j,B2j，…，Btj(j=1,2，…，r)的行数，则

其中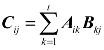，i=1,2，…，s； j=1,2，…，r .

例1 设，，求AB.

解：把A,B分块成

则

而

于是(https://www.daowen.com)

4.几种特殊分块矩阵的行列式和逆矩阵

定义2 设A为n阶方阵，若A的分块矩阵只有在主对角线上有非零子块，其余子块都是零矩阵，且非零子块都是方阵，即

其中Ai(i=1,2，…，s)都是方阵，则称A为分块对角矩阵或准对角矩阵.

分块对角矩阵的行列式具有下述性质：

由此可知，若，则A可逆，且由分块矩阵的乘法可知

这样，就把一个高阶对角矩阵的求逆问题转化为若干个低阶方阵的求逆.

例2 设，求A−1和.

解：把A分块成，，其中，，于是，，，，所以，.

定义3 设A为n阶方阵，把A分块为：

其中Aii(i=1,2，…，s)都是方阵，则称A为分块上三角矩阵.类似地，分块下三角矩阵为：

其中Aii(i=1,2，…，s)都是方阵.

对于分块上三角（下三角）矩阵，有

及

练习题（五）

1.设，，求AB.

2.设，求A−1和.