由于任何可逆矩阵A都可以利用初等行变换化为单位矩阵，而每进行一次初等行变换相当于在左边乘一个同种的初等方阵，所以在利用初等行变换把可逆矩阵A化为单位矩阵时，就相当于找到有限多个初等方阵P1,P2，…，Pt，使

Pt…P2P1A=E.

上式同时在右边乘A−1，得

Pt…P2P1AA−1=EA−1，

即

Pt…P2P1E=A−1.

这表示对A做一系列的初等行变换使之化为E时，对E做同样的一系列初等行变换可以使之化为A−1.把两式合在一起，得

这就是求逆矩阵的另一种重要方法：

即在n阶可逆矩阵A的右边写上与A同阶的单位矩阵E，构成一个n ×2n的新矩阵，然后对它进行一系列的初等行变换，把左半部分化为单位矩阵E，与此同时，右半部分就被化成了A−1.

类似地分析，可以得到利用初等列变换求A的逆矩阵的方法：

构成一个2n ×n的矩阵，然后对它进行一系列的初等列变换，把A化为单位矩阵E的同时E被化成了A−1.即

例10 设矩阵，求A−1.

解：

即

这种方法显然比利用伴随矩阵求逆矩阵简单，并且也不必先判断A是否可逆.如果A不能化为单位矩阵，则A不可逆；如果A可以化为单位矩阵，则A可逆，同时也求出了A−1.方阵的阶数越高时，利用初等行变换求逆矩阵就越显示出其优越性.

利用初等变换也可以去求解一些简单的矩阵方程：

（1）AX=B.

解题方法：当A可逆时，X=A−1B，构造新矩阵，并对矩阵进行一系列的初等行变换，使A化为单位矩阵E的同时矩阵B就化为了A−1B，即

（2）XA=B.

解题方法：当A可逆时，X=BA−1，构造新矩阵，并对矩阵进行一系列的初等列变换，使A化为单位矩阵E的同时矩阵B就化为了BA−1，即

例11 设矩阵A和X满足等式AX=A+2X，其中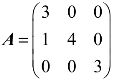，求X.(www.daowen.com)

解：由AX=A+2X可得(A−2E)X=A，

而

构造新矩阵，并对它施行初等行变换：

于是

例12 设A,B均为3阶方阵，且满足A−1BA=6A+BA，且，求B.

解：用A−1右乘方程两边得A−1B=6E+B，即(A−1−E)B=6E，B=6(A−1−E)−1.

从而.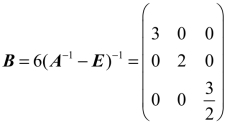

练习题（四）

1.求下面矩阵的秩.

（1）；

（2）.

2.利用初等变换求下面矩阵的逆矩阵.

（1）；

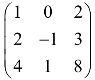（2）.

3.利用初等变换解以下矩阵方程.

（1）；

（2）.

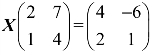4.设矩阵A和X满足等式AX=A+2X，其中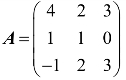，求X.

5.设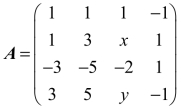，已知r(A)=2，求参数x,y.