定义3 在m ×n矩阵A中任取k行k列，位于这些行列相交处的k2个元素，保持它们原来的相对位置不变，组成一个k阶行列式，称为矩阵A的一个k阶子行列式，简称k阶子式.当子式的值不为零时，称为非零子式.

定义4 矩阵A的最高阶非零子式的阶数r称为矩阵A的秩，记作r(A)=r.

即当矩阵A中存在一个r阶非零子式，而所有超过r阶的子式都为零时，称r为矩阵A的秩.并规定，零矩阵的秩为零.

由定义可知，任何矩阵的秩都是唯一的.

例4 设矩阵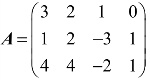，求矩阵A的秩.

解：A的二阶子式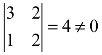是非零子式，而矩阵A的所有三阶子式全都为零：

所以，r(A)=2.

例5 设矩阵A为n阶非奇异方阵，求矩阵A的秩.

解：由题意得，即A的n阶子式是非零子式，于是r(A)=n.

当方阵的秩等于方阵的阶数时，称之为满秩方阵；当方阵的秩小于方阵的阶数时，称之为降秩方阵.显然，可逆方阵、非奇异方阵、满秩方阵是等价的概念.

例6 设矩阵，求矩阵A的秩.

解：A是一个行阶梯形矩阵，其非零行有3行，由此可得A的所有4阶子式全为零.

而，所以，r(A)=3.

事实上，行阶梯形矩阵的秩就等于该矩阵的非零行行数.

定理4 初等变换不改变矩阵的秩.即若A→B，则r(A)=r(B).

求矩阵秩的另一可行方法为：利用初等行变换将矩阵化成行阶梯形矩阵，行阶梯形矩阵的非零行行数就是矩阵的秩.

例7 设矩阵，求矩阵A的秩.

解：对矩阵A作初等行变换化成行阶梯形矩阵：

由行阶梯形矩阵非零行行数为3可知r(A)=3.(www.daowen.com)

关于矩阵的秩，有如下结论：

（1）设A为m ×n矩阵，B是满足有关矩阵运算要求的矩阵，则：

①　r(A)≤min{m,n}；

②　r(A)=r(AT)；

③　r(kA)=r(A)(k≠0)；

④　r(AB)≤min{r(A)，r(B)}；

⑤　r(AB)≥r(A)+r(B)−n ；

⑥　r(A+B)≤r(A)+r(B)；

⑦　AB=O时，r(A)+r(B)≤n，n是A的列数（或B的行数）.

（2）设A为n阶方阵，则：

①　若r(A)=n，则r(A*)=n；

②　若r(A)=n−1，则r(A*)=1；

③　若r(A)＜n−1，则r(A*)=0.

例8 若A是n阶方阵，且A2=A，证明：

r(A−E)+r(A)=n .

证明：由A2=A得(A−E)A=O，故r(A−E)+r(A)≤n ；

又r(A−E)+r(A)=r(E−A)+r(A)≥r(E−A+A)=r(E)=n ；

于是r(A−E)+r(A)=n .