定义 1 当矩阵A与矩阵B的行数与列数分别相等时，称矩阵A、B为同型矩阵.

定义 2 当A=(aij)和B=(bij)都是m ×n矩阵，且aij=bij(i=1,2，…，m； j=1,2，…，n)时，称矩阵A与矩阵B相等，记作A=B.

1.矩阵的加法

设有两个m ×n矩阵A=(aij)与B=(bij)，则矩阵A与B的和记作A+B，规定

注意：只有当两个矩阵是同型矩阵时，才能进行加法运算.即同型矩阵可以相加，其和的元素等于对应元素分别相加.

例1 已知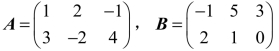，求A+B.

解：.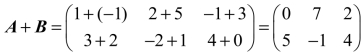

2.矩阵的减法

设有两个m ×n矩阵A=(aij)与B=(bij)，则矩阵A与B的差记作A−B，规定

注意：只有当两个矩阵是同型矩阵时，才能进行减法运算.即同型矩阵可以相减，其差的元素等于对应元素分别相减.

例2 已知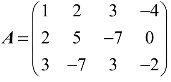，，求A−B.

解：.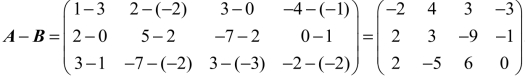

3.矩阵的数乘

设m ×n矩阵A=(aij)，k为常数，则数k与矩阵A的乘积记作kA或Ak，规定(www.daowen.com)

例3 若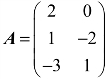，则.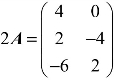

矩阵的加减法与数乘称为矩阵的线性运算，它满足下面的运算律：

（1）A+B=B+A；

（2）(A+B)+C=A+(B+C)；

（3）A+O=A；

（4）(k+l)A=kA+l A；

（5）k(A+B)=kA+kB ；

（6）k(lA)=(kl)A；

（7）1A=A，(−1)A=−A；

（8）0A=O,kO=O.

例4 已知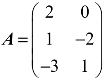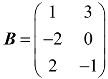，，且A+2X=B，求矩阵X.

解：