矩阵的元素可以全是实数，也可以出现复数，相应地称为实矩阵、复矩阵.本书若无特殊说明，一般讨论的总是实矩阵.下面从矩阵的元素及行数、列数出发，讨论一些特殊矩阵.

1.零矩阵

元素全都是零的矩阵称为零矩阵，记为O.如

这是两个不同的零矩阵.

2.三角矩阵

（1）上三角矩阵：非零元素只出现在主对角线及其上方的方阵称为上三角矩阵，如

（2）下三角矩阵：非零元素只出现在主对角线及其下方的方阵称为下三角矩阵，如

3.对角矩阵

非零元素只出现在主对角线上的方阵称为对角矩阵，如

4.数量矩阵

主对角线上的元素相同，其余元素全为零的方阵称为数量矩阵，如

5.单位矩阵

主对角线上元素全为1，其余元素全为零的方阵称为单位矩阵，记为E，即

6.行矩阵

只有一行的矩阵称为行矩阵，如A=(a1,a2，…，an)是一个1×n矩阵（也称n维行向量）.(www.daowen.com)

7.列矩阵

只有一列的矩阵称为列矩阵，如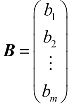是一个m×1矩阵（也称为m维列向量）.

注：行向量和列向量统称为向量，通常用小写希腊字母α 、β 、γ等表示.

8.对称矩阵

对于n阶方阵A=(aij)n×n，如果aij=aji(i,j=1,2，…，n)，则称之为对称矩阵，如

9.反对称矩阵

对于n阶方阵A=(aij)n×n，如果aij=−aji(i,j=1,2，…，n)，则称之为反对称矩阵，如

10.行阶梯形矩阵

满足下列两个条件的矩阵称为行阶梯形矩阵：

（1）若有零行，则零行位于矩阵的最下方；

（2）每个非零行从左到右第一个非零元素之前的零的个数逐行增加.

11.行最简形矩阵

行阶梯形矩阵的每行第一个非零元素全为1，且每行的第一个非零元素所在列的其他元素全为零，则称之为最简行阶梯形矩阵，简称行最简形矩阵.

如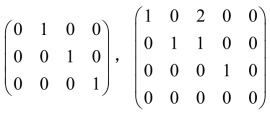都是行最简形矩阵.