定理1（克莱姆法则）含有n个方程的n元线性方程组

的系数行列式D ≠0时，即

线性方程组有唯一解：

分析：克莱姆法则一共有3个结论：1°方程组有解；2°解是唯一的；3°解由公式（1）给出.因此证明的步骤是：

第一，把代入方程组，验证它确实是解，这样就证明了方程组有解，并且（1）式是一个解，即证明了结论1°与3°.

第二，证明如果x1=c1，x2=c2，…，xn=cn是线性方程组的一个解，那么一定有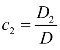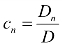，，…，.这就证明了解的唯一性，即证明了结论2°.

证明：设n阶行列式，首先，证明（1）式确实是线性方程组（*）式的解.将行列式Di按第i列展开得：

Di=b1A1i+b2A2i+…+bnAni(i=1,2，…，n)，

其中，Aij是行列式D中元素aij的代数余子式（i，j=1,2，…，n）.现把（i=1,2，…，n）代入第k个方程的左端，得：

这说明将式（1）代入第k（k=1,2，…，n）个方程后，得到了一个恒等式，所以式（1）是线性方程组（*）的一个解.

其次，设x1=c1，x2=c2，…，xn=cn是线性方程组（*）的一个解，那么，将xi=ci代入线性方程组（*）后，得到n个恒等式：

用系数行列式的第i（i=1,2，…，n）列的代数余子式A1i,A2i，…，Ani依次去乘式（2）中n个恒等式，得到：

将此n个等式相加，得：

从而有：ciD=Di，得（i=1,2，…，n）.这就是说，如果（c1,c2，…，cn）是方程组（*）的一个解，那么一定有（i=1,2，…，n），所以方程组只有一个解.

例1　求解线性方程组

解：方程组的系数行列式：

根据克莱姆法则，这个线性方程组有唯一解.又因(www.daowen.com)

所以这个线性方程组的唯一解为：

例2　判断齐次线性方程组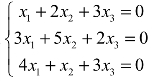解的情况.

解：方程组的系数行列式为

所以根据克莱姆法则，这个线性方程组有唯一解.又因

所以这个线性方程组的唯一解为：x1=0，x2=0，x3=0，此称为唯一零解.

由上得，对含有n个方程的n元齐次线性方程组

（1）当D ≠0时，齐次线性方程组有且仅有唯一零解；

（2）系数行列式D=0时，齐次线性方程组有非零解.（这是充分必要条件）

例3 问λ，μ取何值时，齐次线性方程组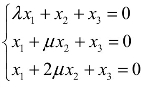有非零解？

解：当

即当λ=−1或μ=0时，原齐次线性方程组有非零解.

注 利用克莱姆法则解线性方程组，有两个前提条件：

（1）方程个数与未知量的个数相等；

（2）系数行列式不等于零.

用克莱姆法则求解系数行列式不等于零的n元非齐次线性方程组，需要计算n+1个n阶行列式，它的手工计算工作量很大.实际上关于数字系数的线性方程组（包括系数行列式等于零及方程个数和未知量个数不相同的线性方程组）的解法，一般都采用后续章节介绍的方法来求解.克莱姆法则主要是在理论上具有重要的意义，特别是它明确地揭示了方程组的解和系数之间的关系.