定理1(LapLace展开式定理) n阶行列式D等于它的任意一行(列)的元素与其对应的代数余子式的乘积之和,即
D=ai1Ai1+ai2Ai2+…+ainAin(i=1,2,…,n),
或
D=a1jA1j+a2jA2j+…+anjAnj(j=1,2,…,n).
证明:只需证明按行展开的情形,按列展开的情形同理可证.
1°先证按第一行展开的情形.
根据性质5有
按行列式的定义有
同理
所以
D=a11A11+a12A12+…+a1nA1n.
2°再证按第i行展开的情形.
将第i行分别与第i-1行、第i-2行、…、第1行进行交换,把第i行换到第1行,然后再按1°的情形,即有
定理1也叫作行列式按行(列)展开法则,此定理表明,n阶行列式可以用n-1阶行列式来表示,因此该定理又称为行列式的降阶展开定理.
例2 计算四阶行列式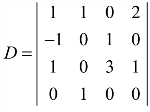 .
.
解:
由上题得,利用此定理并结合行列式的性质,可以大大简化行列式的计算.计算行列式时,一般利用性质将某一行(列)化简为仅有一个非零元素,再按定理1展开,变为低一阶行列式,如此继续下去,直到将行列式化为三阶或二阶.这在行列式的计算中是一种常用的方法,称为降阶法.
例3 计算行列式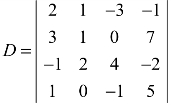 .
.
解:D的第4行已有一个元素是零,利用性质5,有
例4
式中左端叫范德蒙(Vandermonde)行列式.结论说明,n阶范德蒙行列式之值等于a1,a2,…,an这n个数的所有可能的差ai-aj(1≤j<i≤n)的乘积.
证明:用数学归纳法.
1°当n=2时,计算2阶范德蒙行列式的值: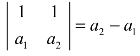 ,可见n=2 时,结论成立.
,可见n=2 时,结论成立.
2°假设对于n-1阶范德蒙行列式结论成立,来看n阶范德蒙行列式:把第n-1行的(-a1)倍加到第n行,再把第n-2行的(-a1)倍加到第n-1行,如此继续,最后把第1行的(-a1)倍加到第2行,得到
后面这个行列式是n-1阶范德蒙行列式,由归纳假设得
于是上述n阶范德蒙行列式等于
根据数学归纳法原理,对一切n≥2,式(1)成立.
定理2 n阶行列式D中某一行(列)的各元素与另一行(列)对应元素的代数余子式的乘积之和等于零,即:
ai1Aj1+ai2Aj2+…+ainAjn=0 (i≠j)
或
a1jA1t+a2jA2t+…+anjAnt=0 (j≠t)(https://www.daowen.com)
证明:只证行的情形,列的情形同理可证.
把行列式D按第j行展开,有
将上式中的ajk换成aik(k=1,2,…,n),
当i≠j时,上式的第i行与第j行的对应元素相同,它的值应等于零,由定理1将D1按第j行展开,有D1=ai1Aj1+ai2Aj2+…+ainAjn=0(i≠j).
定理1和定理2可以合并写成
或
例5 设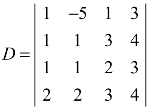 ,求(1)A41+A42+A43+A44;(2)M41+2M42+M43.
,求(1)A41+A42+A43+A44;(2)M41+2M42+M43.
解:
练习题(四)
1.填空题.
(1)行列式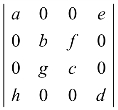 中元素f的代数余子式是________;
中元素f的代数余子式是________;
(2)若 中代数余子式A12=−1,那么A21=________;
中代数余子式A12=−1,那么A21=________;
(3)已知四阶行列式D中第三行元素依次为2,5,3,4;它们的余子式分别为3,1,2,4;则D=________.
2.计算下列行列式.
(1)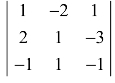 ;
;
(2)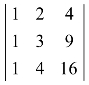 ;
;
(3) ;
;
(4) ;
;
(5)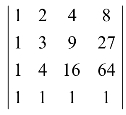 ;
;
(6) .
.
3.计算4阶行列式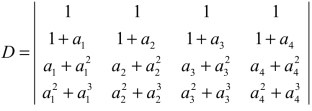 .
.
4.已知行列式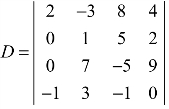 ,试求:
,试求:
(1)D;
(2)A11+A12+A13+A14;
(3)3M13+M23+2M43.
5.设行列式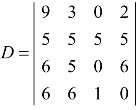 ,求:
,求:
(1)A41+A42+A43+A44;
(2)6A21+9A22+5A24.
6.证明等式: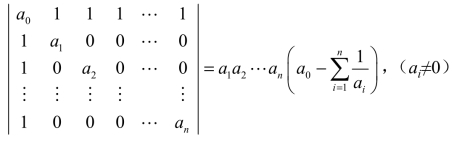 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







