为了给出行列式的定义，先从观察二阶、三阶行列式的特征入手.已知二阶与三阶行列式分别为

可以从中发现以下规律：

（1）二阶行列式是2！项的代数和，三阶行列式是3！项的代数和；

（2）二阶行列式中每一项是取自不同行且不同列两个元素的乘积，三阶行列式中的每一项是取自不同行且不同列的三个元素的乘积；

（3）每一项的符号都取决于位于不同行且不同列的三个元素的下标排列，如

a12a23a31的列标排列231的逆序数 τ（231）=2，231为偶排列，此项符号为正；

a13a22a31的列标排列321的逆序数 τ（321）=3，321为奇排列，此项符号为负.

即当这一项中元素的行标是按自然序排列时，元素列标排列为偶排列时，此项符号为正；为奇排列时，此项符号为负.

作为二、三阶行列式的推广，下面给出n阶行列式的定义.

定义5　由排成n行n列的n2个元素aij(i,j=1,2，…，n)组成的符号称为n阶行列式.它是n！项的代数和，每一项是取自不同行且不同列的n个元素的乘积，各项再乘以一个正、负号：每一项各元素的行标排成自然序排列，若列标的排列为偶排列时，则此项符号为正；为奇排列时，则此项符号为负.于是得n阶行列式按行标自然顺序排列的展开式为：

其中，表示对所有的n级排列j1j2…jn求和；(−1)τ(j1j2…j n)a1j1a2j2…anjn称为行列式的一般项.

特别说明：

（1）行列式是一种特定的算式符号；

（2）n阶行列式是n！ 项的代数和；

（3）n阶行列式的每项都是位于不同行且不同列的n个元素的乘积；

（4）a1j1a2j2…anjn乘 以(−1)τ(j1　j2…jn　)；

（5）一阶行列式 | a |=a，如 |−2 |=−2；

例如：当n=4时，4阶行列式表示4！(=24)项的代数和，因为取自不同行且不同列4个元素的乘积恰有4！项.根据n阶行列式的定义，4阶行列式为

例如：a14a23a31a42行标排列为1234，元素取自不同的行；列标排列为4312，元素取自不同的列，因为 τ（4312）=5，所以该项符号为负号，即−a14a23a31a42是上述行列式中的一项.

例2　在5阶行列式中，a12a35a23a41a54这一项的符号是什么？

解：这一项各元素的行标未按自然顺序排列，应先将此项按行标的自然顺序排列为a12a23a35a41a54，此时列标的排列为23514.因 τ（23514）=4，故这一项符号为正号.

例3　写出4阶行列式中，带负号且包含因子a11a23的项.

解：包含因子a11a23项的一般形式为(−1)t(13j3j4)a11a23a3j3a4j4.

按定义，j3可取2或4，j4可取4或2，因此包含因子a11a23的项只能是a11a23a32a44或a11a23a34a42，但因τ(1324)=1为奇数，τ(1342)=2为偶数，所以此项只能是−a11a23a32a44.

例4　计算上三角行列式.

解：由n阶行列式的定义，应有n！项，其一般项为(−1)τ(j1j2…jn)a1j1a2j2…anjn.

但由于D中有许多元素为零，只需求出上述一切项中不为零的项即可.在D中，第n行元素除ann外，其余均为0.所以jn=n；在第n-1行中，除a(n−1)(n−1)和a(n−1)n外，其余元素都是零，因而jn-1只取n-1、n这两个可能，又由于ann、a(n-1)n位于同一列，而jn=n，所以只有jn-1=n-1.这样逐步往上推，不难看出，在展开式中只有a11a22…ann一项可能不为零.而这项的列标所组成的排列的逆序数是 τ（12…n）=0，故取正号.因此，由行列式的定义有

即上三角行列式的值等于主对角线上各元素的乘积.(www.daowen.com)

同理可得下三角行列式，

特别地，对角行列式.

上（下）三角行列式及对角行列式的值，均等于主对角线上元素的乘积.

例5　计算行列式.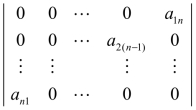

解：这个行列式除了a1na2(n-1)…an1这一项外，其余项均为零，现在来看这一项的符号.列标的n级排列为n(n-1)…21，τ(n(n-1)…21)=0+1+2+…+(n-2)+(n-1)=，所以

同理可得：

n 阶行列式还可以有第二种定义：

定义6　n阶行列式也可以定义为

其中，τ(p1p2…pn)为行标排列p1p2…pn的逆序数，表示对所有的n级排列求和.

n 阶行列式的第三种定义：

定义7　n阶行列式也可以定义为

其中，τ(p1p2…pn)为行标排列p1p2…pn的逆序数，τ(l1l2…ln)为列标排列l1l2…ln的逆序数.

练习题（二）

1.求下列各排列的逆序数.

（1）1234； （2）4132；

（3）34215； （4）51324.

2.写出四阶行列式中，以下各项的符号：

（1）a14a23a31a42； （2）a23a11a42a34.

3.计算下列行列式.

（1）；

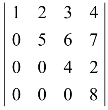（2）；

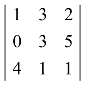（3）；

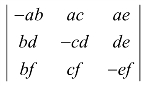（4）.

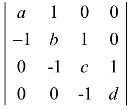4.由行列式的定义计算中x4与x3的系数，并说明理由.

5.计算n阶行列式.

（1）；

（2）.