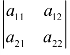定义1 由4个数a11,a12,a21,a22及双竖线“”组成的符号称为二阶行列式.其中aij表示这个元素所在位置为第i行第j列.

构成：二阶行列式含有两行、两列.横排的数构成行，纵排的数构成列.行列式中的数称为行列式的元素，相等的行数和列数“二”称为行列式的阶.

含义：它按规定的方法表示元素a11,a12,a21,a22的运算结果，即为：由左上至右下的两元素之积a11a22，减去右上至左下的两元素之积a12a21.其中每个积中的两个数均来自不同行且不同列.

或者说：二阶行列式是这样的两项的代数和，从左上角到右下角的对角线（又叫行列式的主对角线）上两个元素的乘积减去从右上角到左下角的对角线（又叫副对角线）上两个元素的乘积，即：

此称为对角线法则.

一般将行列式记为D，取自行列式的英文单词determinant的首字母，后面还会用det（·）表示对·做行列式计算.

例1　求的值.

解：.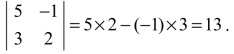

例2　当λ为何值时，行列式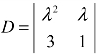的值为0？

解：因为，要使λ(λ−3)=0，须使λ=0或λ=3，即知，当λ=0或λ=3时，行列式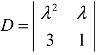的值为0.

于是，将二元线性方程组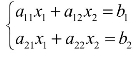 的解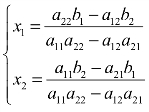中 的两个不同分子，以及一个共同的分母，按其在方程组中的排列方法，以及二阶行列式的运算规律，可令：解中的分母，亦称方程组的系数行列式，为(www.daowen.com)

解中未知数x1的分子，亦称x1的分子行列式，为

解中未知数x2的分子，亦称x2的分子行列式，为

其中，系数行列式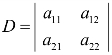是由方程组中两未知数x1、x2的系数按其原有的相对位置排列而成的；x1的分子行列式是将系数行列式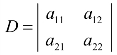中的第1列换成方程组的常数项而得到；x2的分子行列式则是把系数行列式中的第2列换成方程组的常数列而得到.

这样用行列式来表示方程组的解，就得到如下简便、整齐，便于记忆与运算的形式（称为克莱姆法则），即当D≠0时成立

例3　求解二元线性方程组.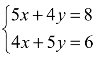

解：由于系数行列式，知该方程组有解，

再由于，，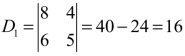

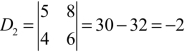得方程组的解为，.

似乎这样表示线性方程组的解比原来更为烦琐，但这创造了多元线性方程组解的公式及其规律性的解法，并为用计算机程序求解多元线性方程组打下了良好的基础；更为下一步学习矩阵知识，为学习高级、大型的管理知识做好了准备.