假设没有外力场，速度分布函数f只与速度有关，即f = f (c)，Boltzmann方程(6.37)变为

可以看出，只要全积分区域上有

(6.58)就成立.

在方程(6.59)两边取对数，可得如下方程：

这说明了ln f是一个碰撞不变量. 可以证明任何碰撞不变量能够表示成5个基本碰撞不变量(φi = m，mc，mc2/2，i = 1，2，3，4，5)的线性组合：

其中 α，β，γ 是常量. 由(6.61)可得

如果给定系统的单位体积内的分子n，平均速度u和每个分子的平均热力学能3RT/2:

则由条件(6.63)–(6.65)可以确定α，β，γ，然后代入(6.62)，可得

这就是空间均匀的定态Maxwell分布. 它代表气体的平衡状态. n，u和T都是常量，分别是数密度、流速及动力学温度(在热平衡情形下就是热力学的绝对温度).

在(6.62)中，一般情况下，参数 α，β，γ 不是常量，而是空间位置x和时间t的函数，这时 (6.62)仍满足(6.58). 但是Boltzmann方程的左边不一定等于零，这时称(6.66)为Boltzmann方程的局部平衡解.

下面我们找使Boltzmann方程的左边和右边(等号右边已等于零)同时等于零的α，β，γ:

由(6.62)可得

假设外力场F与c无关，将(6.68)代入(6.67)中，得到

为了简便，在上面的表达式中使用了求和规定：如果在同一项里出现相同下角标，则从1到3求和，比如 aibi = a1b1 + a2b2 + a3b3. 比较等式(6.69)两边的c的同次幂的系数，有

由(6.73)说明了 γ 只是时间t的函数:

在方程(6.72)的两边求关于xi的导数，并利用结论(6.74)，可推出

在上式中将下角标i，j，k依次轮换，可以得到如下方程:

先(6.76) + (6.77)，然后减去(6.75)，得到

因此，

将(6.79)代入(6.72)，得

因此，

其中ωik是一个反对称张量，即ωik=-ωik. 将(6.79)及(6.80)代入(6.71)，可以得到

在(6.81)的两边求关于xi的导数，有

在上式中交换角标i，k后与(6.82)相减，得到(www.daowen.com)

由于ωik是一个反对称张量，即ωik = -ωki，上式变为

所以Fk可以表示成如下形式:

其中φ = φ(x，t)是一个势函数. (6.85) 说明只有当外力等于一个保守力和一个非保守力之和时，Boltzmann方程(6.67)才有(6.68)形式的解. 将(6.85)代入(6.81)，可以得到

所以

其中ζ是任意函数. 将 (6.85) 及 (6.87) 代入 (6.70)，就得到存在Maxwell形式的解(6.68)的条件:

如果外力场是稳定的保守势场，那么ωkj是一个常数，而且φ = φ(x)与t无关. 这时，(6.88)变为

现在讨论两种特殊情况:

(i) 设φ(x)是一个四次可微函数，将(6.89)依次对xl，xm，xn求导可以得到

其中l，m，n都可以取为1，2或3. 在(6.90)中含有7个未知量，即，3个ikω和3个iξ；但(6.90)含有这7个未知量的10个方程构成方程组. 7个未知量本身与位置x无关，但它们的系数与x有关，因此，除了势函数满足特定的关系之外，一般来说，此方程组的系数行列式不等于零. 此通常方程组(6.90)只有平凡解:

于是，由(6.79)和(6.80)知βi=0，进而由(6.89)知

这说明了ζ是常数. 所以，由(6.87)得

最后，由(6.68)可知

因此，该气体的状态是Maxwell–Boltzmann分布:

其中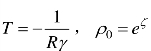. (6.93)右边是与t无关的函数，这说明了在稳定的保守势场中，Boltzmann方程的严格平衡解只能是稳定的Maxwell-Boltzmann分布.

(ii) 假定势函数φ(x)的三阶导数都等于零，则方程组(6.90)可能有非平凡解. 因此,假设

其中Blm =Bml. 将(6.94)代入(6.89)，并比较方程两边的x的同次幂系数，可得

(6.95)–(6.97)是只含8个未知量ζ，ξi，γ，ωim 的10个方程. 尽管如此，很容易发现，当Bli = Bδli时，上面的方程组有平凡解. 事实上，这时方程(6.97)变为

因此

上式中c0，c1，c2是常数. 从方程(6.96)求得

其中是常数. 最后，从方程(6.95)中求出

上式中c是常数. 上面的计算中用到了AiAlω il=0，因为ωil是一个反对称张量.

由方程(6.99)–(6.101)可知，在稳定的简谐力场中，系统可以保持一种振荡的Maxwell分布状态，而振荡的频率中含有场的本征频率和它的二倍频率. Boltzmann最先得到此结论.