在本节中，考虑由同一种分子组成的气体，即简单气体. 用f表示速度分布函数. 速度分布函数f是位置矢量x，分子速度c和时间t的函数. 在t时刻，那些位于体积元x，dx内且它的速度在c，dc范围内的可能的分子数目为

用m表示分子的质量，mF表示作用在每个分子上的外力. 如果任意一个分子在dt时间内不发生碰撞，则每个分子在时间dt内从原位置移动到位置x + cdt，速度从c变为c + Fdt. 因为没有分子之间的碰撞，故这些分子(f(x,c,t )dxdc )过时间dt后将全部既不增加也不减少地移动到x + cdt，它们的速度变为c + Fdt. 根据分布函数的定义有

但是，一般说来，第二群的分子总数f (x + cdt，c + Fdt，t + dt)dxdc不等于原来第一群的分子总数f(x,c,t)dxdc ，这是因为分子之间的碰撞会使原来第一群的分子改变速度，偏离它们的轨道，同时，其他分子改变轨道(因碰撞)进入第二群，成为第二群的分子. 因此，在碰撞存在的情况下，应有下式:

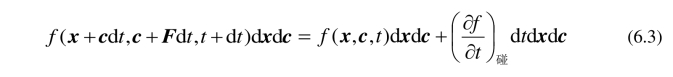
其中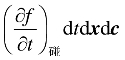表示在某一个固定位置处由碰撞引起的速度分布函数的变化率. (6.3)两边除以dc dtdx，并令dt趋于零，可以推出Boltzmann方程:

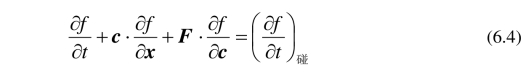
其中表示关于空间的梯度，表示关于速度的梯度. 可以把Boltzmann方程改写为

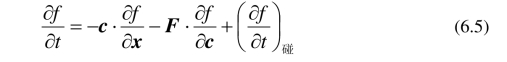
上式说明了速度分布函数在空间某一点处的变化率是两部分的和.

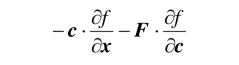
表示由运动和受外力引起的增加的部分. 另一部分是代表由碰撞而增加的部分.

下面讨论和速度分布函数f之间的关系.可以用含未知(速度分布)函数f的积分来表示. 所以Boltzmann方程是含未知函数f的微分和积分的方程. 用

表示在dt时间内由碰撞而进入x，c附近dxdc的分子数，用

表示由碰撞而离开x，c处的区域dxdc的分子数. 因此

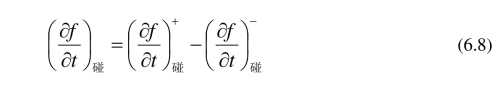
在本节中，假设气体是稀薄气体，即只考虑二体碰撞，忽略不计三体或三体以上的碰撞的几率.

假设质量为m1和m2的两个相互碰撞的分子是光滑、球对称的，并可以看成力心点. 另外，还认为当两个分子相碰撞时，外力远远小于碰撞时的作用力，因此在碰撞过程中可以忽略外力. 用1c，c2和1c′，c2′分别表示分子1和2的碰撞前后的速度. 令

G是两个分子组成的系统的质心速度.

由动量守恒定律和能量守恒定律，有

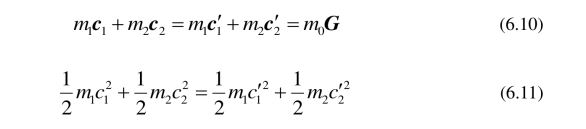
其中m0 = (m1+ m2).

用g和g′分别表示碰撞前后第二个分子相对于第一个分子的相对速度，于是

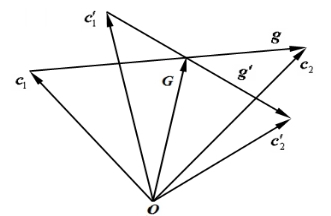
图6.4　分子碰撞中相对速度的变化

根据(6.9)，(6.12)和(6.13)知可以用G，g，1g表示1c，c2和1c′，c2′:

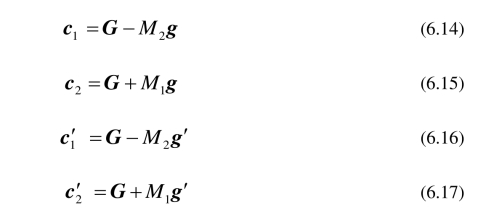
将(6.14)–(6.17)代入能量守恒式(6.11)可得

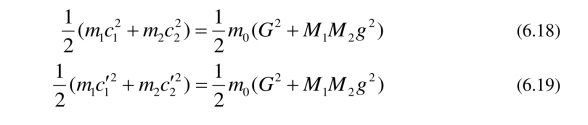
因此有

其中M1 = m1/(m1+ m2)，M2 = m2/(m1+ m2).

在二体碰撞中，为了方便假设分子1静止不动，位于如图6.5所示的O点. 相对于分子1，分子2以速度g相对运动，即分子2的相对速度等于g. 选取以O为原点的球坐标，极轴平行于g. b表示g至极轴的距离，称为碰撞参数. 用g′表示碰撞后分子2相对于分子1的相对速度. g和g′所在平面与初始平面夹角及g与g′的夹角分别记为ε和χ. 过O点作平行于g′的一条直线，则ε如图6.5所示. 以Ω表示g′方向的单位矢量，即Ω 等于g′/g. dΩ表示立体角元，即(www.daowen.com)

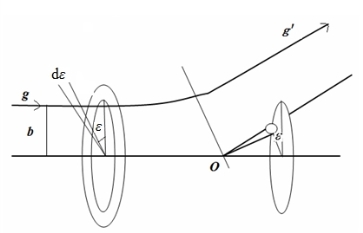
图6.5　分子互相碰撞示意图

由于设分子1在O点不动，分子2碰撞前相对于O点以相对速度g运动. 在dt时间内能与分子1碰撞的分子(即能到达面积元bdbdε上的分子)应在以bdbdε为底面，以-gdt为棱的柱体中，即这些分子2必须在gbdbdεdt的体积中，才能于dt时间内到达面积元bdbdε ,如图6.6所示.

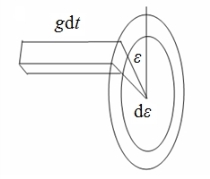
图6.6　分子1附近的状况

速度在c1，dc1，位置在x，dx范围内的分子1的分子数为 f1(x，c1，t) dc1dx. 每个分子1与体积gbdbdεdt中的分子2发生碰撞. 对每个分子1的这样的体积(gbdbdεdt)中有f2(x，c2，t)gbdbdεdtdc2个分子2. 所以在时间段dt内，碰撞总数为

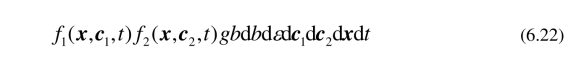
分子1和分子2碰撞后，速度分别变为1c′和c2′，故这两个分子不在原来的速度范围c1，dc1和c2，dc2. 因此，因碰撞而损失的分子数等于碰撞总数. 根据的定义，对所有可能的b，ε，c2积分，并除以dxdt得

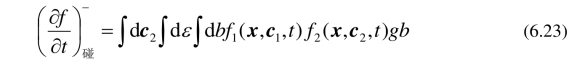
记

σ称为微分碰撞截面，或称微分散射截面，它是g和χ的函数，即σ = σ(g，χ).

上面讨论了这样的碰撞(称为正碰撞)：速度为c1的分子1和速度为c2的分子2碰撞后速度分别变为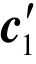和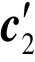. 这时，碰撞前的相对速度g碰撞后变为g′(碰撞后的相对速度). 当然存在这样的碰撞，称为第一对碰撞(正碰撞)的逆碰撞或反碰撞：速度为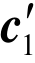的分子1和速度为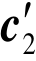的分子2碰撞后速度分别变为c1和c2. 这时，碰撞前的相对速度g′碰撞后变为g(碰撞后的相对速度).

用类似于求(6.22)的方法可求出在dt时间内，在(x，dx)内发生的逆碰撞次数为

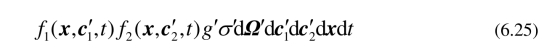
其中Ω′表示g′方向的单位向量，σ′可以用σ代替. 利用(6.9)和(6.14)–(6.17)可推出

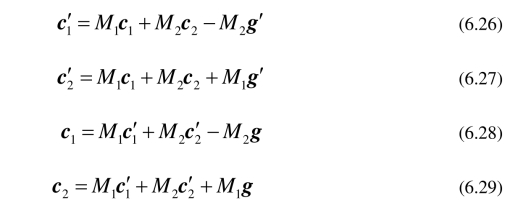
利用(6.26)–(6.29)可以证明

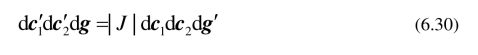
又

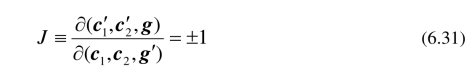
即

成立. 因此可把逆碰撞次数(6.25)表示为

对所有可能的c2和Ω积分，可得因逆碰撞而增加的第一类(c1，dc1)分子的增量：

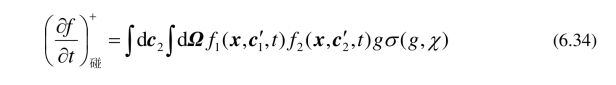
由(6.8)，(6.23)，(6.24)和(6.34)可推出

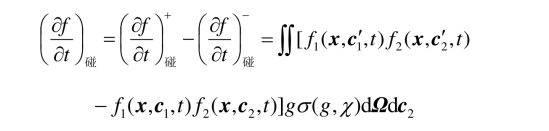
因为我们只讨论简单气体(只有一种分子组成的气体: m1 = m2)，所以也可以把上式表示为

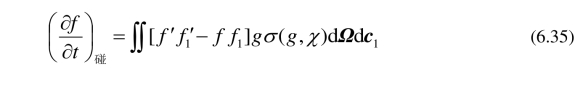
其中

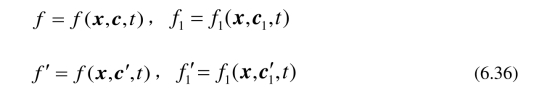
将(6.35)代入(6.4)，得

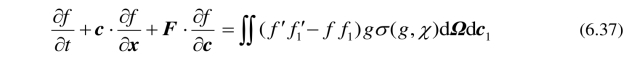
这就是单组分稀薄气体速度分布函数满足的著名的Boltzmann方程（非线性微分–积分方程).