宏观量是能够观测到的物理量,如气体温度、压力、速度和分子通量等. 在统计学中这些量可以用速度分布函数表示出来.
气体的密度(单位体积内的质量)ρ(x,t)可定义为
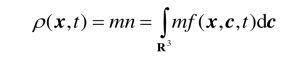
对于单组分(简单)气体,流体速度(气体宏观速度)和平均分子速度是相等的:
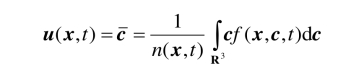
有时,我们在与流体一起运动的坐标系中研究流体力学问题. 这时,分子在运动坐标系中的运动速度为
![]()
称C为特征速度或热速度. 对单组分(简单)气体来说,特征速度的平均值等于零,因为
![]()
单位质量气体的内能e可定义为
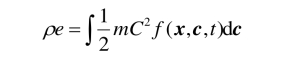
在气体分子运动论中,定义温度T为
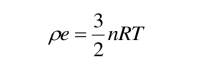
下面讨论分子通量. 根据速度分布函数的物理意义,在Δt时间内,通过面积元AΔ(垂
直于x3轴)的分子数为
![]()
其中cΔtAΔ
3是圆柱体的体积,如图6.2所示.
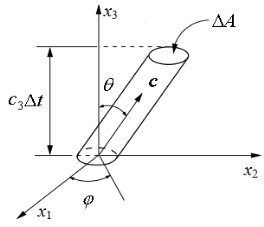
图6.2 通过面积元ΔA的分子通量
分子通量可定义为在单位时间内通过单位面积的分子数,即
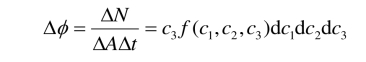 (https://www.daowen.com)
(https://www.daowen.com)
利用Maxwell分布和坐标变换可以计算出总的分子通量:
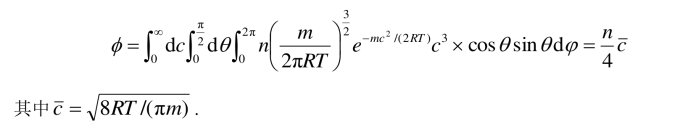
众所周知,容器壁面受到的压力是由气体分子的动量传递引起的. 如果分子与壁面碰撞是弹性的,即弹性碰撞,则碰撞前后速度的大小不变,只是改变方向,切向分量不变,法向分量变成相反(即由c3 变为-c3). 因此,一个分子与壁面发生碰撞后,动量的改变量为2mc3,从而可得出单位时间、单位面积内的动量改变量为

对所有可能的速度积分,可得总的压力为

当f满足Maxwell分布时,可以证明p=nRT成立.
在简单的剪切流中,流体被限制在两个平行板之间,流体满足无滑移物、无渗透边界条件. 在x3 = 0平面静止不动,在x3 = L处的平面以常速运动,c = (0,c2 (x3),0). 该速度剖面是线性的,如图6.3所示.
位于x3处的界面上的动量传递等于该界面的上面和下面层处的分子动量之差. 令θ是分子速度矢量和x3轴之间的夹角. 一个分子与另一个分子发生碰撞之前行走的距离等于平均自由程. 位于x3 − l cos θ和x3 + l cos θ的分子的动量之差为
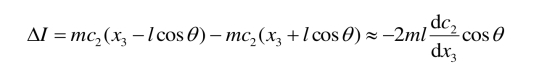
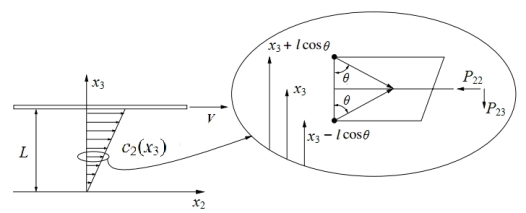
图6.3 简单剪切流的速度剖面
利用分子通量公式,可以算出所有分子的动量传输:
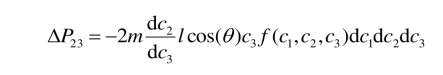
ΔP23代表单位时间内通过单位面积的动量,即压力. 该压力作用在垂直于x2轴的界面,并平行于x3轴. 对所有可能的速度积分后可以得到总的压力分量P23:

其中
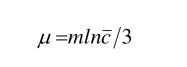
称为气体的黏性系数. 代入l和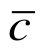 的表达式,得
的表达式,得
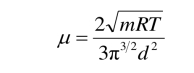
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







