分子运动论研究由大量的分子组成的气体,这些分子在大多数时间间隔内相互独立地运动. 如果没有外力,分子做直线运动. 当两个分子相互碰撞或与壁面碰撞时,分子的碰撞破坏分子直线运动. 如果相比分子的动能,分子的势能可以忽略,则称这种气体为稀薄气体,否则称为稠密气体.
为了更好地理解稀薄气体,假设分子是直径为d的硬球. 众所周知,当温度等于273.15K,压力为102.325 Pa时,1摩尔比稀薄气体占有的体积和该体积内的分子总数分别等于VM=2.24×10-2m3和NA =6.022×1023分子/mol. 在这种情况下,分子(有时称为粒子)数密度n=NA /VM≈2.68×1025分子/m3.我们可以认为每个分子占有体积为VC=1/n≈3.72×10-26m3的正立方体空间. 因此,分子占有的空间的边长为D = (VC)1/3≈3.34×10-9m,它代表分子之间的平均距离.
设一个分子以相对平均速度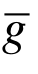 在数密度为n的气体中运动. 由图6.1可以看出,该分子在单位时间内与底面积为2πd,高度为
在数密度为n的气体中运动. 由图6.1可以看出,该分子在单位时间内与底面积为2πd,高度为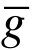 的圆柱内的其他分子发生碰撞. 因此,碰撞频率为ν=nπ 2
的圆柱内的其他分子发生碰撞. 因此,碰撞频率为ν=nπ 2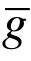 . 平均自由时间为τ=1/ν=1/(nπd 2
. 平均自由时间为τ=1/ν=1/(nπd 2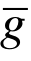 ). 一个分子与其他分子不发生碰撞的平均距离,即分子的两次碰撞之间的平均距离,称为平均自由程,记为l. 当气体处于平衡态时,有
). 一个分子与其他分子不发生碰撞的平均距离,即分子的两次碰撞之间的平均距离,称为平均自由程,记为l. 当气体处于平衡态时,有
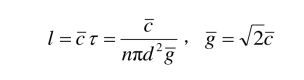
其中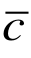 是分子的平均热速度,第二个等式在平衡态气体中成立. 也就是说,在平衡态气体中平均自由程为
是分子的平均热速度,第二个等式在平衡态气体中成立. 也就是说,在平衡态气体中平均自由程为
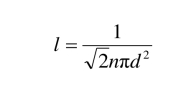
该公式说明了平均自由程与分子数密度成反比,也与分子直径的平方成反比. 注意,对离平衡态不远的情况也可以用该公式.
由完全相同的质量为m的分子组成的气体称为单组分气体或简单气体. 我们一般采用统计学的方法研究气体,因为单位体积的气体是由大量的无序分子构成的. 在标准状态下,1cm3气体中大约含有3×1019个气体分子. 因此,用统计学的方法描述比大量分子的精确描述简单得多.
假设P(x)是几率密度,x = (x1,x2,…,xn),P(x)dx表示x处于x和x + dx之间的几率.dx是体积元(dx = dx1dx2…dxn). 同时几率满足
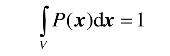
其中V是x的整个变化范围.(www.daowen.com)
假设φ(x)是任意给定的函数,那么我们可以利用几率密度表示φ(x)的均值(或平均值):
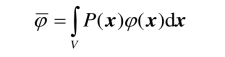
以后用符号“ˉ”表示平均值.
假设气体分布在空间区域V ⊆ R3中,在t时刻分子处于状态点(x,c,t)的概率密度为P(x,c,t),则分子在状态(x,c,t)附近出现的概率为P(x,c,t)dxdc. P(x,c,t)还满足
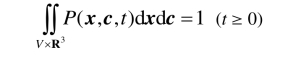
设f (x,c,t) = NP(x,c,t),称f为速度分布函数. 由上式可知函数f满足
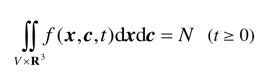
N是V内气体分子的总数. f(x,c,t)表示在时刻t,那些位于体积元x,dx中而且速度范围在c,dc内的分子的几率数. 根据以上讨论可知,t时刻,在x处单位体积内的气体分子数,即数密度为
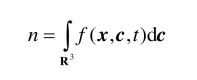
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








