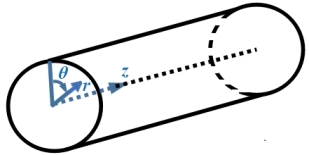
本章中,我们考虑圆管道内的一个时间周期压力驱动流. 假设流体为二元电解质流体,边界上出现速度滑移,管道半径为 a. 建立柱面坐标系 (r,θ,z),坐标原点在管道中心,z轴与流动方向平行. 这里滑移长度依赖于壁面电荷密度:
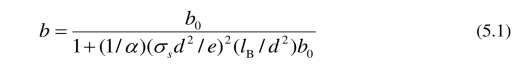
其中 b0 是原滑移长度,它独立于壁面电荷密度,α~1,e 是基本电荷,d 是Lennard-Jones 势的平衡距离, lB = e2/(4πεkBT ),ε 是电解质溶液的介电常数. kB 是 Boltzmann 常数,T 是绝对温度.
双电层电势分布满足泊松方程

其中eρ是局部净电荷密度,对对称电解质溶液,当正负离子数浓度满足 Boltzmann 分布时,局部净电荷密度eρ 可用双电层电势φ表示为
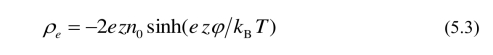
其中 n0 是离子浓度,z 是离子化合价. 对低 zeta 势的情形,利用 Debye–Hückel 近似,得sinh(ezφ/(kBT )) ≈ ezφ/(kBT ),再应用方程 (5.2) 和 (5.3),我们能得到下面的线性化Poisson-Boltzmann 方程其中应用了 ρe = -εκ2φ,ζ 是 zeta 势,κ=[εkBT/(2z2e2n0)]-1/2 是 Debye–Hückel 参数,代表双电层厚度的倒数.
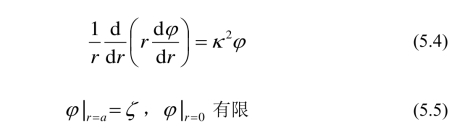
在时间周期压力梯度 cos(ωt)∂p0/∂z 的作用下,产生 z 方向的单向流,ω 代表振荡频率,t 是时间. 假设流体是粘性不可压牛顿流体. 由连续性方程可得 ∂u/∂z=0,所以 u 只是r 和 t 的函数. 因此,动量守恒方程变为
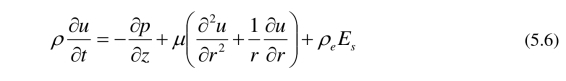
其中 ρ 是流体密度,μ 是黏性系数,Es是流动电势的电场强度,p = cos(ωt)p0 是时间周期压力.边界条件是

其中滑移长度b满足方程 (5.1).
 (www.daowen.com)
(www.daowen.com)
图5.1 圆管道内的时间周期压力驱动流
根据电荷守恒律,总壁面电荷应等于流体的净电荷,因此
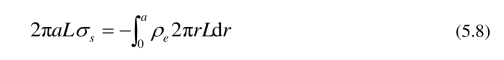
L代表管道长度. 根据方程 (5.2),(5.8) 和边界条件 (5.5),有

将方程 (5.9) 代入方程 (5.1),得
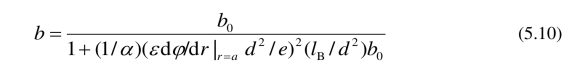
管道内流动电流 ( streaming current) 为

流动电势的电场强度Es 引起反向传导电流 Ic,使得管道内总电流等于零,即
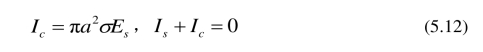
其中σ=2z2e2Dn0/(kBT )是电导率,D 是电解质溶液中离子的扩散系数.
由方程 Is+ Ic=0可得流动电势的电场强度:
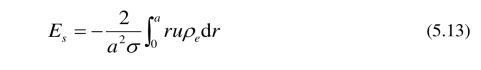
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






