微纳流体力学是指微尺度(特征长度小于或约等于100μm)和纳米尺度(特征长度小于或约等于100nm)通道内的流体的流动和传质传热.

李战华等人在《微流控芯片中的流体流动》一书中提到在微纳流动中连续性介质假设仍适用. 目前，很多理论研究都用连续介质流体方程组来描述微纳流动. 连续介质流体方程组包括连质量守恒方程(又称连续性方程)、动量守恒方程和能量守恒方程. 当流体是粘性不可压牛顿流体时，可把控制方程表示为

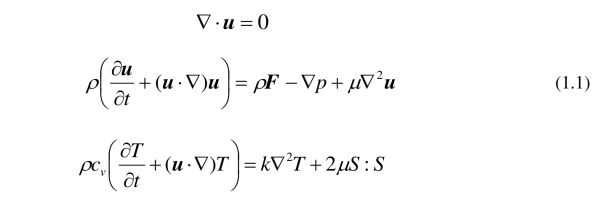
其中u=(u,v,w)是速度，ρ是质量密度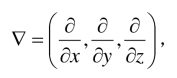，cv是等容比热，k是热传导系数，μ是动力学黏性系数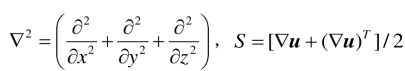，是变形速度张量. 本文中没给出公式 (1.1) 的推导过程，大家可以参考其他流体力学教材.

柱坐标系和球坐标系中的连续性方程和动量守恒方程介绍如下:

在柱坐标系中:

连续性方程

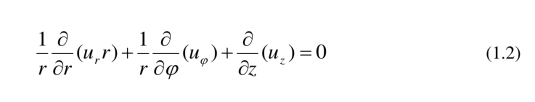
动量守恒方程

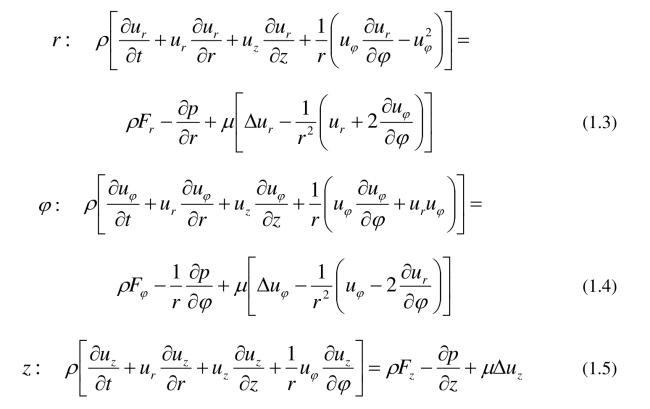
这里,

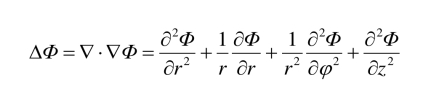
在球坐标系中:

连续性方程

动量守恒方程

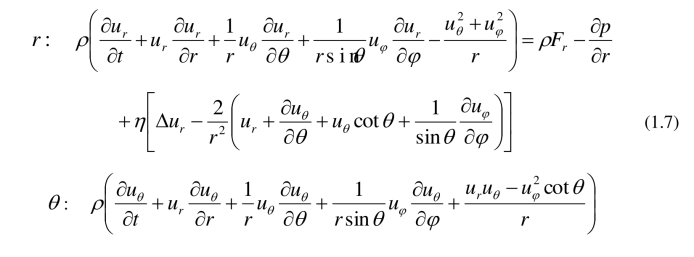(www.daowen.com)

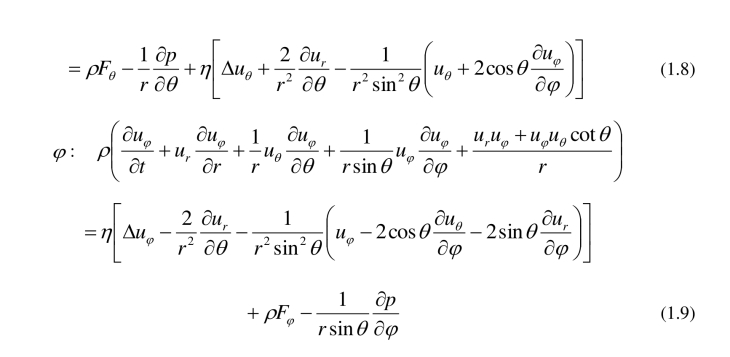
当大多数管道固壁与极性溶液接触时，在两相的接触面上产生电荷. 产生壁面电荷的原因有多种: 极性溶液在电离作用下能产生电荷，离子溶解作用、吸附作用或电子亲和力作用等也都能产生电荷. 壁面电荷吸引溶液中的异性离子，排斥同性离子，从而在溶液中形成带有净电荷的双电层. 基本结构如图1.1所示. 双电层由紧密层和扩散层组成.

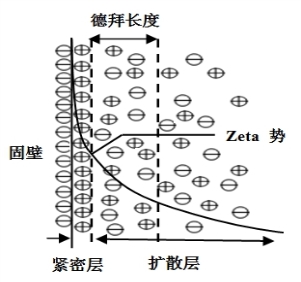
图1.1　双电层

双电层电势分布 ψ 和电荷密度 ρe 满足经典泊松方程:

其中 ε0 是流体的介电系数，e是基本电荷，ni 是第i 类离子的数量浓度，zi 是第i 类离子的化合价. 在热平衡状态中，双电层电势分布和离子浓度满足Boltzmann分布:

kB 是Boltzmann常数，ni∞ 是第i类离子远离壁面处 (ψ=0) 的数量浓度.

对于对称电解质溶液有

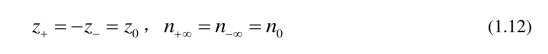
将 (1.11) 代入 (1.10) 得

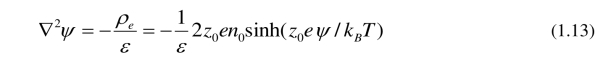
我们假设在边界上双电层电势ψ等于常数ζ，即ψ=ζ(zeta势).

在压力驱动流中，液体携带双电层的电荷一起运动。这种非电场力作用下的随流电荷运动叫流动电流(streaming current)，电荷的运动在微通道两端形成电势差，称为流动电势(streaming potential)，其负梯度称为流动诱导电场。流动诱导电场作用在双电层的净电荷上，产生一个与流动方向相反的电场力，使得流量小于传统流体动力学理论计算的流量，好像流体具有更大的粘度，这就是微通道内的电粘性效应 (electroviscous effect)。此外，由于流体在微通道中的流动会形成流动电流和流动电势，在这一过程中它将机械能和化学能转换为电能。